Задача 11637 ...

SOVA

17.11.2016

В правильной треугольной пирамиде SABC высота равна 12, а апофема равна 20. Точки Р и Т - середины рёбер SB и SC соответственно. Плоскость α содержит прямую РТ и параллельна высоте пирамиды SH.

а) Докажите, что плоскость α делит высоту основания ВВ1 в отношении 1:2, считая от вершины В
б) Найдите расстояние от точки В до плоскости α

Пирамида правильная, в основании равносторонний треугольник АВС, Н- центр основания.
АН=НВ=НС.
РТ- средняя линия треугольника SBC
PT || BC, значит PT || плоскости АВС.
Плоскость α проходит через РТ и пересекает плоскость АВС. Значит линия пересечения плоскостей MN параллельна РТ

SH⊥ пл. АВС
плα || SH, значит пл. ⊥ пл. АВС
Их линия пересечения KF || SH
KF- cредняя линия треугольника SA1H и потому делит А1H пополам.
А1F=FH

MN- средняя линия треугольника ВНС.
MN делит ВН пополам.
ВЕ=ЕН
Так как точка Н делит медиану ВВ1 в отношении 2:1, считая от вершины, то
ВЕ=ЕН=НВ1
ВЕ:ЕВ1=1:2

б) Из треугольника SA1H по теореме Пифагора
А1H=sqrt(20^2-12^2)=16
A1Н=В1Н
ВЕ=ЕН=НВ1=16

Расстояние от точки В до плоскости α равно расстоянию от точки В до прямой MN.
Это расстояние равно расстоянию между параллельными прямыми ВС и МN
d=A1F=A1H/2=16/2=8


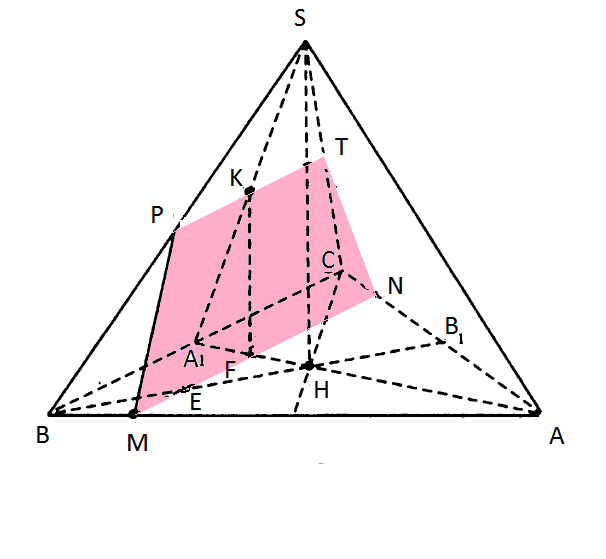
Ответ: 8