Задача 11587 ...

SOVA

16.11.2016

Найти число корней уравнения cos4x-3cos((3π/2)-2x)+2sin^23x+2cos^23x=0, принадлежащих отрезку [-π/2;π]

По формулам приведения
cos((3π/2)-2x)=-sin2x.
Основное тригонометрическое тождество
sin^23x+cos^23x=1
cos4x=1-2sin^22x.
Уравнение принимает вид:
2sin^22x-3sin2x-3=0.
Квадратное уравнение относительно sin2x.
Замена переменной
sin2x=t
2t^2-3t-3=0
D=9+24=33
t=(3-sqrt(33))/4 или t=(3+sqrt(33))/4
Так как |sin2x| меньше или равно 1, остается решить только одно уравнение
sin2x=(3-sqrt(33))/4
Решаем графически.
Строим график у=sin2x и график у=(3-sqrt(33))/4
Cм. рисунок.
О т в е т. 4 корня на отрезке [-π/2;π]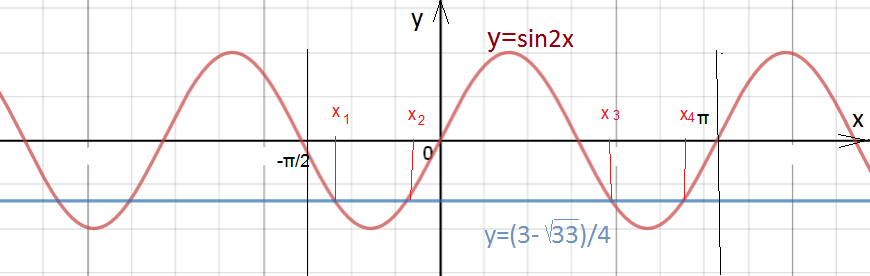

Ответ: О т в е т. 4 корня на отрезке [-π/2;π]