Задача 11561 Найдите все значения параметра a, при...
Условие
system{x^2+y^2=a;2xy=a-1}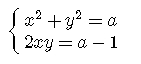
Решение
Получим систему
{x^2+y^2=a
{2xy=x^2+y^2-1
или
{x^2+y^2=a
{(x-y)^2-1=0
Второе уравнение равносильно совокупности двух уравнений, значит вся система равносильна совокупности двух систем
1)
{x^2+y^2=a
{x-y=1
или
2)
{x^2+y^2=a
{x-y=-1
Решаем первую способом подстановки
x^2+(x-1)^2=a
x^2+1-2x+x^2=a
или
2x^2-2x-(а-1)=0
D=4+4*2(а-1)=4+8а-8=8a-4
Уравнение имеет один корень при а=1/2
При D > 0 уравнение имеет 2 корня
x_(1)=1-sqrt(2a-1) или x_(2)=1+sqrt(2a-1)
2)
Решаем вторую систему способом подстановки
x^2+(1+x)^2=a
x^2+1+2x+x^2=a
или
2x^2+2x-а+1=0
D=4+8(a-1)=8a-4
Уравнение имеет .
x_(3)=-1-sqrt(2a-1) или x_(4)=-1+sqrt(2a-1)
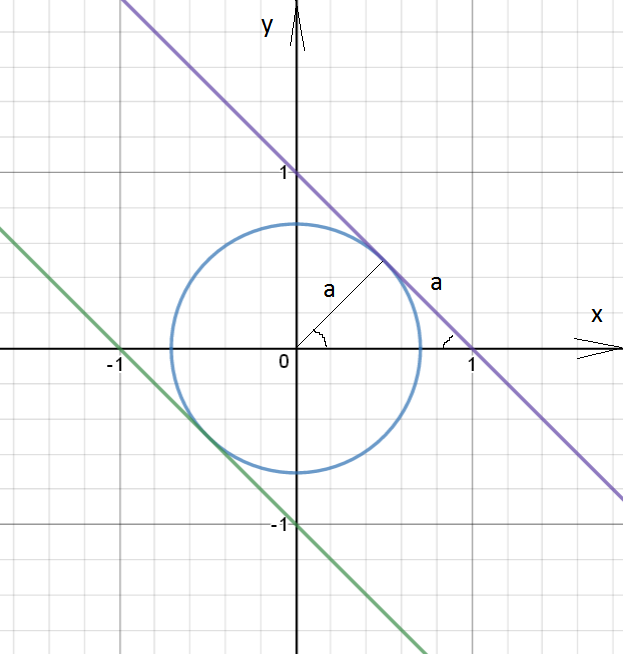
Чтобы решений было ровно два, необходимо и достаточно, чтобы было две точки пересечения окружности и гиперболы
О т в е т. а=1/2