Задача 11521 А) Может ли разность квадратов двух...
Условие
Б) Может ли разность кубов двух натуральных чисел равняться квадрату натурального числа?
В) Найдите все простые числа, каждое из которых равно разности кубов двух простых чисел.
Решение
10^2-6^2=4^3
64=64-верно.
Б) a^3-b^3=c^2
(a-b)*(a^2+ab+b^2)=c*c
Слева произведение двух множителей и справа произведение двух множителей.
Равенство возможно в следующих случаях
a-b=c
a^2+ab+b^2=c
Возводим первое равенство в квадрат, понимая, что при возведении возможно появление посторонних корней.
a^2-2ab+b^2=c^2
a^2+ab+b^2=c
Вычитаем
-3ab=c^2-c
Равенство невозможно, так как с^2-c > 0
Второй случай
a-b=1
a^2+ab+b^2=c^2
a=b+1
(b+1)^2+(b+1)b+b^2=c^2
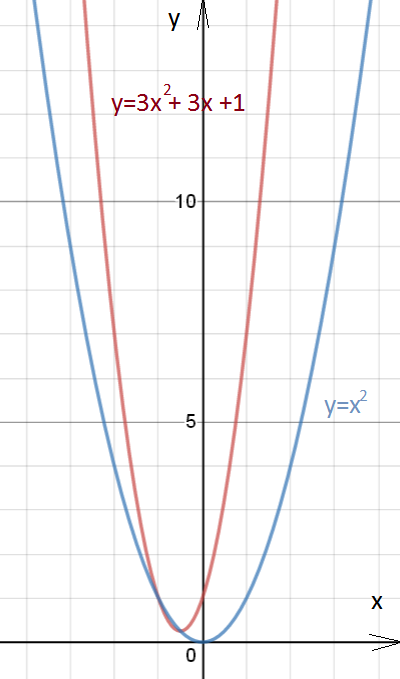
3b^2+3b+1=c^2
Равенство возможно при отрицательных b, натуральных чисел нет
Cм. рисунок.
В) 3^3-2^3=19
Других пар нет, так как
a^3-b^3=c^2
(a-b)*(a^2+ab+b^2)=c^2
Равенство возможно при a-b=1
a=b+1
Нет простых чисел следующих одно за другим.
Так как среди двух следующих одно за другим натуральных чисел, одно обязательно четное.