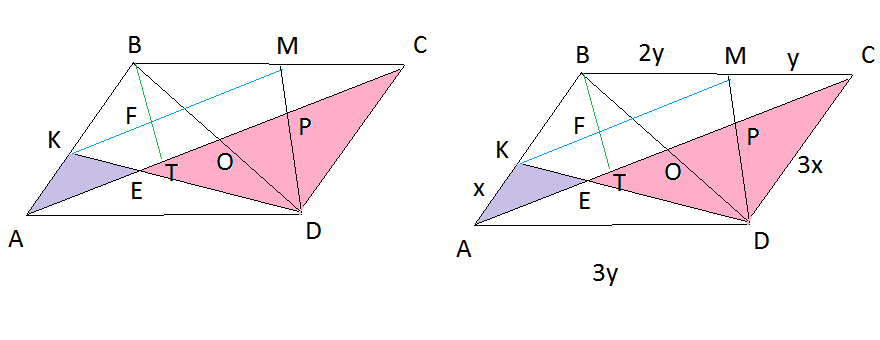
Задача 11518 На диагонали AC параллелограмма ABCD...

slava191

13.11.2016

На диагонали AC параллелограмма ABCD отмечены точки Е и Р, причем АЕ:ЕР:РС=1:2:1. Прямые DE и DP пересекают стороны АВ и ВС в точках К и М соответственно.

А) Докажите, что КМ || АС.

Б) Найдите площадь параллелограмма АВСD, если известно, что площадь пятиугольника ВКЕРМ равна 30.

SOVA

13.11.2016

★

А) Диагонали параллелограмма в точке пересечения делятся пополам.
АО=ОС
AE=EO=EP=РС=АС/4
Треугольники АКЕ и ЕСD подобны по трем углам.
Углы при сторонах АК и СD- внутренние накрест лежащие.
Углы при вершине Е - вертикальные.
Значит. АК:СВ=AE:EC=1:3.
Пусть АК=х, тогда СD=3x
AB=CD=3x
ВК=2x
Аналогично, МРС и АРВ подобны.
МС=y, AD=3y,
BC=AD=3y
BM=2y
Стороны треугольников ВКС и ВАС, составляющие угол В, пропорциональны, угол В- общий,
КМ=2/3 АС.
КМ|| АС.

Б)

S (четырехугольника ВЕКМР) = (1/2)*S (параллелограмма АВСD) - S(АКЕ)-S(МРС).
Значит,
S (АВСD)=2S(ВЕКМР)+2S(АКЕ)+2S(МРС)
Обозначим
S (АВСD)=S
S=2*30+2*(AЕ*FT+РС*FT)
Из подобия треугольников АКМ и АВС.
ВF:BT=2:3
FT=(1/3)ВТ
(AЕ*FT+РС*FT)=
=(AE+PC)*(1/3)BT=(1/6)AC*BT=(1/6)*(1/2)S=(1/12)S

S=2*30+(1/6)S
(5/6)S=60
S=360/5
S=72
О т в е т. S=72