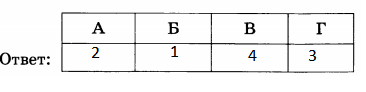
Задача 11434 Каждому из четырёх неравенств в левом...

slava191

10.11.2016

Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

[b]НЕРАВЕНСТВА[/b]

А) (x-3)^3 < 0
Б) 2^(1-2x) > 0,5
В) log(1/3)x < -1
Г) (x-1)^3(x-3) < 0

[b]РЕШЕНИЯ[/b]

1) x < 1
2) x < 3
3) 1 < x < 3
4) x > 3

SOVA

10.11.2016

★

А) (x–3)^3 < 0
x-3 < 0
x < 3
О т в е т. 2) х < 3

Б) 2^(1–2x) > 0,5
2^(1-2x) > 2^(-1)
Показательная функция с основанием 2 возрастающая, большему значению функции соответствует большее значение аргумента
1-2х > -1
-2x > - 2
x < 1
О т в е т. 1) x < 1

В) log_(1/3)x < –1
log_(1/3)x < –1*log_(1/3)(1/3)
log_(1/3)x < log_(1/3)(1/3)^(-1)
log_(1/3)x < log_(1/3)3
Логарифмическая функция с основанием (1/3) убывающая, большему значению функции соответствует меньшее значение аргумента
x > 3
и учитывая ОДЗ логарифмической функции, получаем
систему неравенств:
{x > 3
{x > 0
О т в е т. 4) х > 3

Г) (x–1)^3(x–3) < 0
Решаем методом интервалов:

__+__ (1) ___-__ (3) ___+__

О т в е т. 3) (1;3) или 1 < x < 3