Задача 1142 В равнобедренном треугольнике ABC с...

slava191

13.05.2014

В равнобедренном треугольнике ABC с углом 120 градусов при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E - на отрезке AB.
a) Доказать, что FH=2DH
б) Найдите площадь DEFH, если AB=4.

а)
1) PD перпендикулярно AB, тогда DH=DP
2) Угол AED=30 градусов
3) DP=1/2DE
Значит FH=2DH
б)
AM=ABsin?ABC=2
BC=2ABcos?ABC=4sqrt(3)
Пусть DH=EF=x, FH=ED=2x
треугольник ABC подобен треугольнику AED, следовательно
AN/AM=ED/BC
(2-x)/2=2x/4sqrt(3)
x=3-sqrt(3)
S=DE*DH=2x^2=24-12sqrt(3)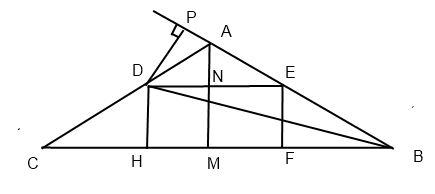

Ответ: 24-12sqrt(3)