Задача 11314 Каждому из четырёх неравенств в левом...
Условие
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий номер решения. 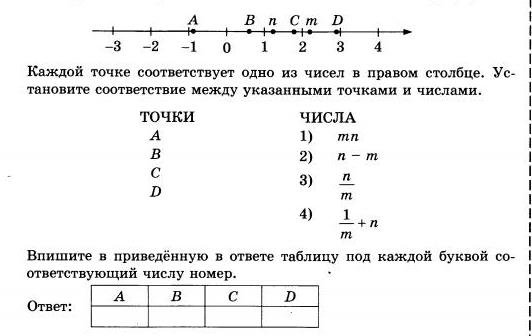
Решение
Отмечая на координатной прямой значения х, при которых данное выражение равно 0(х=1, х=3), получаем 3 интервала : (-∞;1),(1;3),(3;+∞)
На интервалах (-∞;1) и (3;+∞) значение выражения положительно, на интервале (1;3) - отрицательно.
Значит, х∈(1;3). (А-1)
Б)(x-3)^2/(x-1) > 0
Отмечая на координатной прямой значения х, при которых данное выражение равно 0(х=3) и при котором данное выражения не имеет смысла(знаменатель равен нулю при х=1), получаем 3 интервала : (-∞;1),(1;3),(3;+∞)
На интервале (-∞;1) значение выражения отрицательно, на интервалах (1;3) и (3;+∞) - положительно.
Значит, х∈(1;3)⋃(3;+∞). (Б-2)
В)(x-1)^2(x-3) < 0
Отмечая на координатной прямой значения х, при которых данное выражение равно 0(х=1, х=3), получаем 3 интервала : (-∞;1),(1;3),(3;+∞)
На интервале (3;+∞) значение выражения положительно, на интервалах (-∞;1) и (1;3) - отрицательно.
Значит, х∈(-∞;1)⋃(1;3). (В-3)
Г)(х-1)/(х-3) > 0
Отмечая на координатной прямой значения х, при которых данное выражение равно 0(х=1) и при котором данное выражения не имеет смысла(знаменатель равен нулю при х=3), получаем 3 интервала : (-∞;1),(1;3),(3;+∞)
На интервалах (-∞;1) и (3;+∞) значение выражения положительно, на интервале (1;3) - отрицательно.
Значит, х∈(-∞;1)⋃(3;+∞)
(Г-4)
Ответ: 1234