Задача 11304 Найдите все значения параметра а, при...
Условие
log^2_(2)|4-x^2|-2a*log2|x^2-4|+a+6=0
имеет ровно четыре различных корня.
Решение
x∈(-бесконечность; -2)U(-2;2)U(2 ;+бесконечность).
Замена переменной
log_(2)|x^2-4|=t,
так как |x^2-4|=|4-x^2|
log^2_(2)|4-x^2|=t^2
Квадратное уравнение
t^2-2at+a+6=0
имеет ровно два корня при любых значениях а, так как
D=(-2a)^2-4*(a+6)=4a^2-4a-24=4(а^2-a-6) > 0
(а+2)(а-3) > 0
a∈(-бесконечность;-2)U(3;+ бесконечность)
Пусть корни t1 и t2.
Обратная замена приводит к уравнениям
log_(2)|x^2-4)|=t_(1) или log_(2)|x^2-4)|=t_(2)
x^2-4=±2^(t_(1)) или x^2-4=±2^(t_(2))
Так как 2^(t_(1)) > 0 и 2^(t_(2)) > 0 при любых t1 и t2, то каждое из уравнений x^2=4+2^(t_(1)) и x^2=4+2^(t_(2))
имеет по два корня.
Всего 4 корня.
Чтобы выполнялось требование задачи, два других уравнения не должны иметь корней.
Для этого необходимо, чтобы
4-2^(t_(1)) и 4-2^(t_(2)) были отрицательными числами, значит оба корня t1 и t2 должны быть больше двух.
Найдем при каких значениях параметра а оба корня квадратного уравнения
t^2-2at+a+6=0
больше двух.
Необходимо и достаточно выполнения трех условий:
1) D > 0
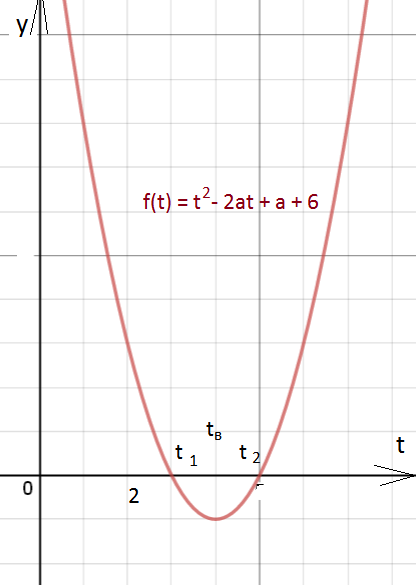
2) f(2) > 0, где f(t)=t^2-2at+a+6
3) t_(в) > 2, t_(в)=(2а/2)=a - абсцисса вершины параболы f(t)=t^2-2at+a+6
(см. рисунок)
1) a∈(-бесконечность;-2)U(3;+ бесконечность)
2) 2^2-4a+a+6 > 0
3) a > 2
Из системы неравенств:
{ a∈(-бесконечность;-2)U(3;+ бесконечность)
{-3a+10 > 0
{ a > 2
или
{ a∈(-бесконечность;-2)U(3;+ бесконечность)
{a < 10/3
{a > 2
получаем ответ
О т в е т. (3;10/3)