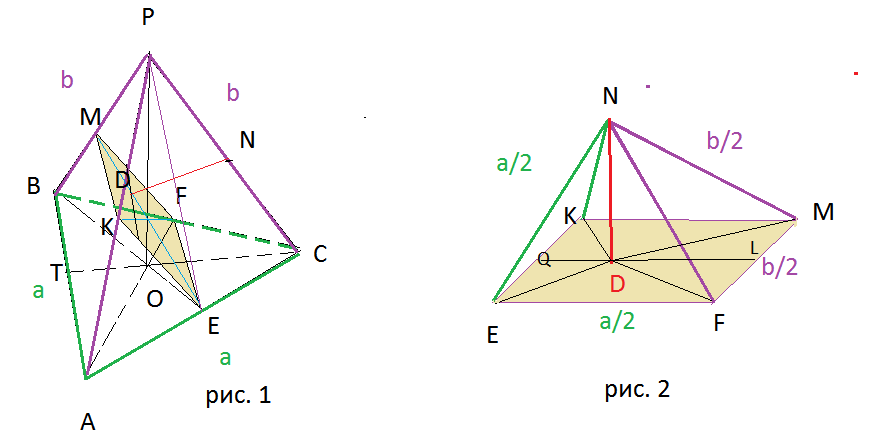
Задача 11300 В правильной пирамиде PABC точки Е, F,...

slava191

06.11.2016

В правильной пирамиде PABC точки Е, F, K, M, N - середины ребер АС, ВС, РА, РВ и РС соответственно.

А) Докажите, что объем пирамиды NEFMK составляет четверть объема пирамиды PABC.

Б) Найдите радиус сферы, проходящей через точки N, Е, F, M, K, если известно, что АВ=8, АР=6.

SOVA

08.11.2016

★

Пирамида РАВС - правильная, Δ АВС - равносторонний, высота пирамиды проектируется в точку О -центр окружности, описанной около треугольника АВС.
Пусть АВ=ВС=АС=а; РА=РВ=РС=b.
Тогда АО=ОВ=ОС=a*sqrt(3)/3 и по теореме Пифагора
PO^2=b^2-(a*sqrt(3)/3)^2=b^2-(a^2/3)=(3b^2-a^2)/3
PO=sqrt(3b^2-a^2)/sqrt(3)
V(PABC)=(1/3)*S(Δ ABC)*PO=
=(1/3)*(a^2sqrt(3)/4)* sqrt(3b^2-a^2)/sqrt(3)=
=a^2*sqrt(3b^2-a^2)/12

Проводим MK||AB и FE || AB - средние линии треугольника АРВ и АВС.
МК=FE=a/2

Проводим KE||PC и MF || PC - средние линии треугольника АРC и BPC.
КE=MF=b/2

Так как СТ - высота, медиана и биссектриса равностороннего треугольника, СТ⊥АВ и OC - проекция PС, то по теореме о трех перпендикулярах РС⊥АВ
Значит и прямые параллельные РС перпендикулярны АВ.

KE⊥МК и MF⊥МК

ЕFМК - прямоугольник со сторонами (а/2) и (b/2).
Пирамида NEFMK ( см. рис. 2), ребра которой NE=NK=a/2
NF=NM=b/2
Равные наклонные имеют равные проекции, поэтому
ED=DK и FD=MD , точка D принадлежит оси симметрии прямоугольника QL:
EQ=QK=b/4
D- основание высоты ND.
Пусть QD=x, тогда DL=(a/2)-x
Из прямоугольного треугольника EDN:
ED^2=(b/4)^2+x^2
Из прямоугольного треугольника NDF:
DF^2=(b/4)^2+((a/2)-x)^2
ND^2=NE^2-ED^2 и ND^2=NF^2-DF^2.
Приравниваем правые части и находим QD:
QD=(2a^2-b^2)/4a.
Тогда
ND^2=(3a^2b^2-b^4)/16a^2
ND=b*sqrt(3a^2-b^2)/4a
v(NEFMK)=(1/3)*S(EKMF)*ND=(ab/12)*(b*sqrt(3a^2-b^2)/4a)=b^2*sqrt(3a^2-b^2)/48
Не совсем так как надо.
Должно получиться (1/4)*(a^2*sqrt(3b^2-a^2)/12)=
=a^2*sqrt(3b^2-a^2)/48.