Задача 11295 Ребро куба ABCDA1B1C1D1 равно 2sqrt(5)....
Условие
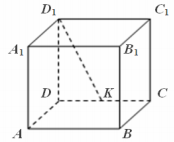
Решение
Значит, для того чтобы найти расстояние между двумя скрещивающимися прямыми, нужно через одну из прямых провести плоскость, параллельную второй прямой. Из любой точки первой прямой опустить перпендикуляр на плоскость и найти его длину.
Проводим A1M, М- середина АВ.
Плоскость МА1D1K || AD, так как A1D1 || AD и КМ || AD.
Находим расстояние от точки D до плоскости.
Проводим DF⊥D1K
Так как треугольник DD1K- прямоугольный,
DD1=2sqrt(5)
DK=sqrt(5)
По теореме Пифагора
D1K^2=DD1^2+DK^2=(2sqrt(5))^2+(sqrt(5))^2=25
D1K=5
D1K*DF=DD1*DK
DF=2*sqrt(5)*sqrt(5)/5=2
О т в е т. 2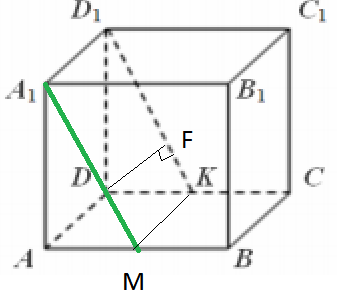
Все решения
Поэтому находим площадь прямоугольного треугольника:
2·√5·√5/2=5
Находим гипотенузу по т. Пифагора:
D1K=5
Находим высоту через площадь и гипотенузу, проведенную к гипотенузе (она же и является расстоянием между прямыми AD и D1K):
h=5*2/5
h=2
Ответ: 2