Задача 11237 ...

slava191

11 марта 2016 г. в 00:00

Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.

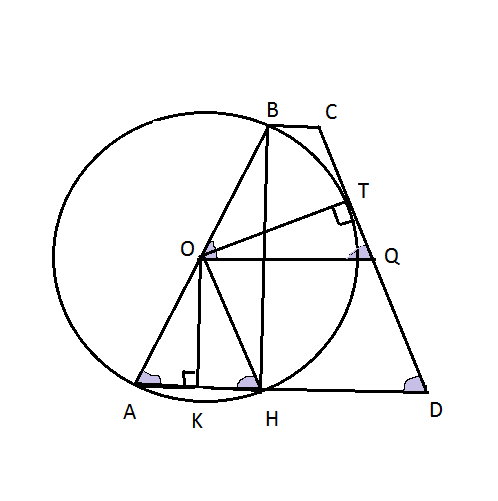
а) Докажите, что четырёхугольник DQOH — параллелограмм.

б) Найдите AD, если ∠BAD=60° и BC=2.

SOVA

11 апреля 2016 г. в 00:00

★

а)
АО=ОВ=ОТ=ОH=R
ВС=AB⇒ CQ=QD=R
OH=QD=R
∠OAH=∠OHA (Δ OAH – равнобедренный ОА=ОН=R)
∠OAH=∠QDH – углы при основании равнобедренной трапеции.
∠OHA=∠QDH – соответственные углы равны ⇒ OH|| QD.
HOQD– параллелограмм, две стороны которого OH и QD параллельны и равны.

б)Δ OAH – равносторонний, углы при основании 60 ° ⇒ АН=R ⇒ AK=KH=R/2
Так как трапеция равнобдренная, то АН=FD=R
По теореме Пифагора
ОК=R√3/2

Δ ОАК подобен Δ OTD
OA:OQ=OK:OT
R:OQ=(R√3/2):R
OQ=2R√3/3

OQ– cредняя линия трапеции АВСD.

OQ=(BC+AD)/2=(2+2+2R)/2=2+R
Приравниваем и находим R
2+R=2R√3/3
R=6/(2√3–3)
AD=2+2R=2+(12/(2√3–3))=2+8√3+12=8√3+14
О т в е т. AD=8√3+14.