Задача 11236 ...

slava191

03.11.2016

В кубе ABCDA1B1C1D1 все рёбра равны 5. На его ребре BB1 отмечена точка K так, что KB=4. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.

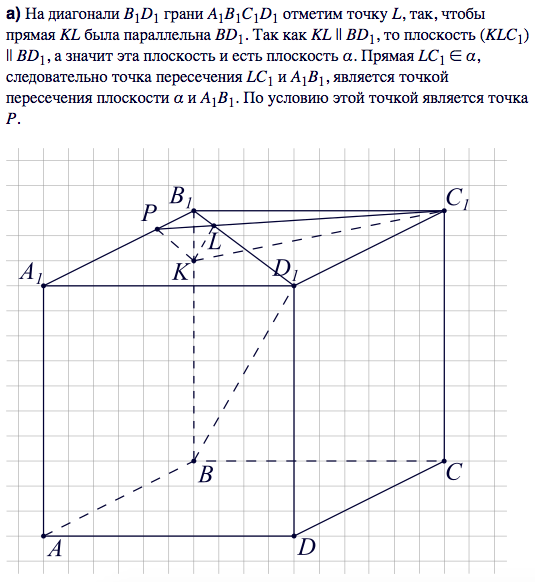
а) Докажите, что A1P:PB1=3:1, где P — точка пересечения плоскости α с ребром A1B1.

б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.

Ответ: arctg sqrt(26)/4

SOVA

04.11.2016

★

а) В диагональной плоскости ВВ1D1D проводим КF||BD1.
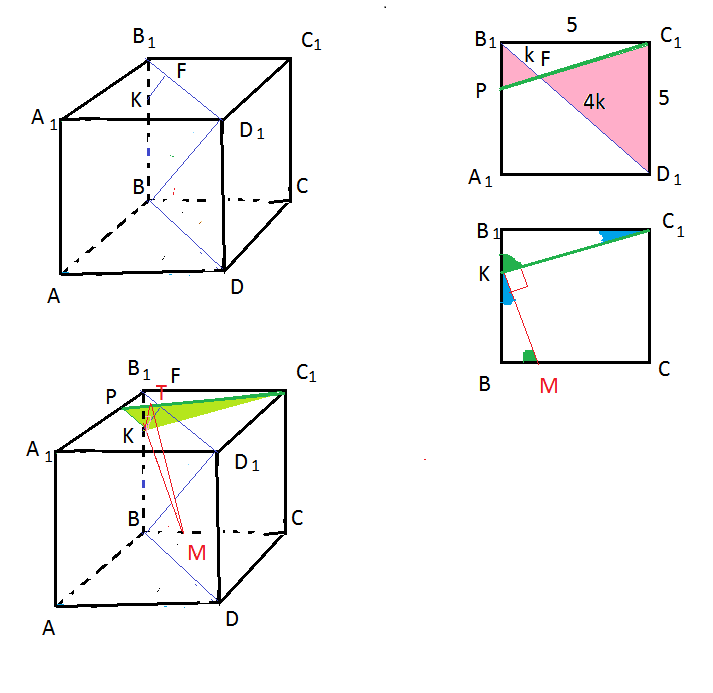
В1F:FD1=1:4 по теореме Фалеса.
В верхней грани А1В1С1D1 проводим С1Р до пересечения с А1В1.
Плоскость α - плоскость С1PK.
Δ B1PF подобен Δ C1DF по двум углам.
B1P:C1D1=B1F:FD1
B1P:5=1:4
B1P=5/4
A1P=5-(5/4)=15/4
A1P:PB1=(15/4):(5/4)=3:1.

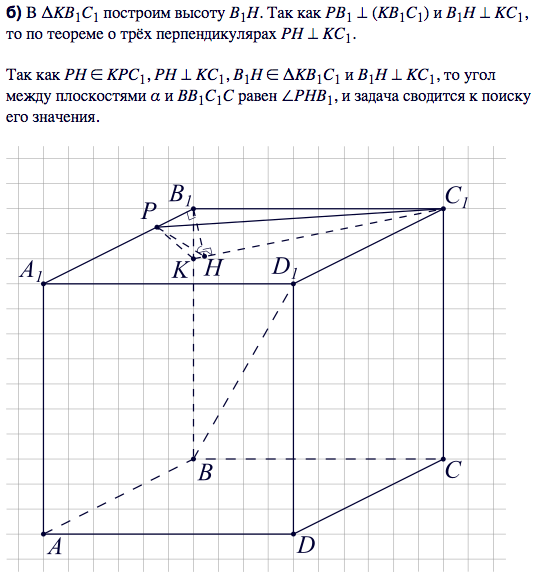
б)
Плоскость α и грань BB1C1C пересекаются по отрезку КС1.
Чтобы построить линейный угол двугранного угла проводим перпендикуляры к линии пересечения КС1.
МК⊥КС1
ТК⊥КС1
∠ТКМ- линейный угол двугранного угла.
Треугольники КВМ и В1С1К подобны по двум углам.
ВМ:В1К=КВ:С1В1
ВМ=4/5
КТ - высота треугольника PKC1 cо сторонами
РК=sqrt(41)/4
KC1=sqrt(26)
PC1=5sqrt(17)/4
Угол не нашла