Задача 11229 а) Найдите корень уравнения...
Условие
б) Найдите все корни этого уравнения, принадлежащие промежутку [-Pi/2; Pi/2]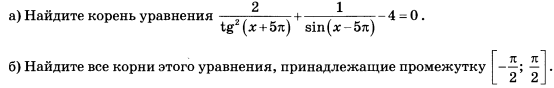
математика 10-11 класс
9950
Решение
★
tg(5π+x)=tgx
Уравнение принимает вид
(2cos^2x/sin^2x)-(1/sinx)-4=0
или
{2cos^2x-sinx-4sin^2x=0;
{sinx≠0.
Решаем первое уравнение
6sin^2x+sinx-2=0
D=1+48=49
sinx=-2/3 или sinx=1/2
x=arcsin(-2/3)+2πk, k∈Z;
x=π-arcsin(-2/3)+2πn, n∈Z
или
x=(π/6)+2πm, m∈Z;
x=π-(π/6)+2πs, s∈Z.
О т в е т.
а)x=-arcsin(2/3)+2πk, k∈Z;
x=π+arcsin(2/3)+2πn, n∈Z
или
x=(π/6)+2πm, m∈Z;
x=(5π/6)+2πs, s∈Z.
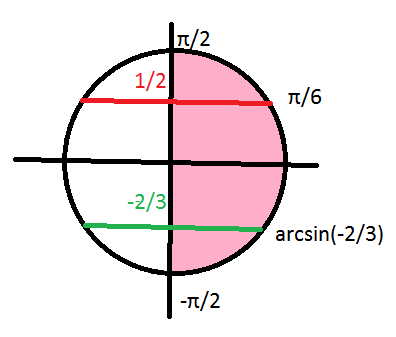
б) Указанному промежутку принадлежат два корня:
arcsin(-2/3) и(π/6).