Задача 11148 В треугольнике АВС биссектриса ВЕ и...

larisashakirova

01.11.2016

В треугольнике АВС биссектриса ВЕ и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника АВС.

Рассмотрим треугольник ABD. ВО является биссектрисой и высотой, значит треугольник ABD равнобедренный и AB=BD. Следовательно, AO=OD=AD/2=96/2=48. AD медиана, значит BD=CD = > AB=BD=CD.
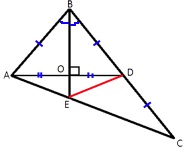
Проведем отрезок ED и рассмотрим треугольник BEC.
ED - медиана этого треугольника, так как делит сторону BC пополам.
Площади треугольников EDC и EDB равны (по свойству медианы). SEDC=SEDB=(BE*OD)/2=(96*48)/2=2304
SABE=(BE*AO)/2=(96*48)/2=2304 = > SABC=3*2304=6912.
AD - медиана треугольника ABC (по условию), следовательно делит треугольник на два равных по площади треугольника ABD и ACD (по свойству медианы).
SABD=(AD*BO)/2 = > BO=72.
Рассмотрим треугольник ABO, он прямоугольный, тогда применим теорему Пифагора:
AB^2=BO^2+AO^2
AB^2=2304+5184
AB^@=7488
AB=24√13
BC=2AB=48√13
Рассмотрим треугольник AOE.
OE=BE-BO=96-72=24
Так как этот треугольник тоже прямоугольный, то можно применить теорему Пифагора:
AE^2=AO^2+OE^2
AE^2=2304+576
AE^2=2880
AE=24√5
Так как BE - биссектриса, то используя ее свойство запишем:
AE/EC=AB/BC
24√5/EC=24√13/48√13 = > EC=48√5
AC=24√5+48√5=72√5



Ответ: 24√13, 48√13, 72√5