Задача 11145 Расстояние от точки пересечения...

larisashakirova

01.11.2016

Расстояние от точки пересечения диагоналей до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.

Пусть диагональ АС=68, ОН=17. Диагонали ромба точкой пересечения делятся пополам, поэтому АО=34. Рассмотрим треугольник АОН. Он прямоугольный. По определению синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе: sin∠OAH=OH/AO=17/34=1/2. Значит ∠OAH=30°. Диагонали ромба являются биссектрисами его углов, поэтому ∠ВАD=60°. ∠А+∠В=180° = > ∠B=180-60=120°. Противолежащие углы ромба равны, значит ∠С=60°, ∠D=120°.

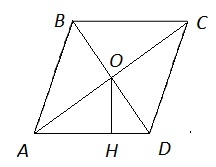
Ответ: 60° и 120°