Условие
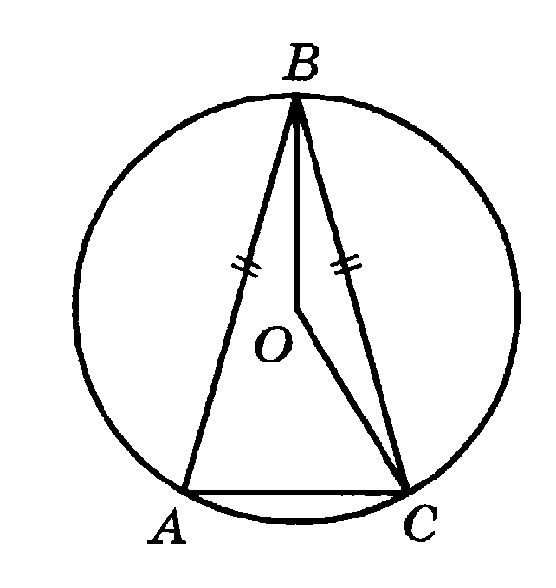
Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ=ВС и ∠АВС=28°. Найдите величину угла ВОС. Ответ дайте в градусах.
математика 8-9 класс
8018
Решение
Угол ВОС является центральным, а угол ВАС - вписанным, значит градусная мера угла ВОС в два раза больше градусной меры угла ВАС, т.е. ∠ВОС=2∠ВАС. Треугольник АВС равнобедренный с основанием АС. Значит ∠ВАС=∠ВСА как углы при основании. По теореме о сумме углов треугольника 2∠ВАС=180-28=152° = > ∠ВОС=152°.
Ответ: 152
Все решения
Вписанный ∠ АВС=28* опирается на дугу АС=56*( по свойству вписанного угла)
Дуга ВС= дуге АВ=(360*-56*)/2=152* (Равные хорды стягивают равные дуги).
∠ ВОС=152* как центральный опирающийся на дугу ВС=152*.
Ответ: 152*
Написать комментарий

