Задача 11028 ...

slava191

29.10.2016

В неравнобедренном треугольнике АВС угол BAC = 45°. Продолжение биссектрисы CD треугольника пересекает описанную около него окружность θ_(1) в точке Е. Окружность θ_(2), описанная около треугольника АDE, пересекает продолжение стороны АС в точке F.

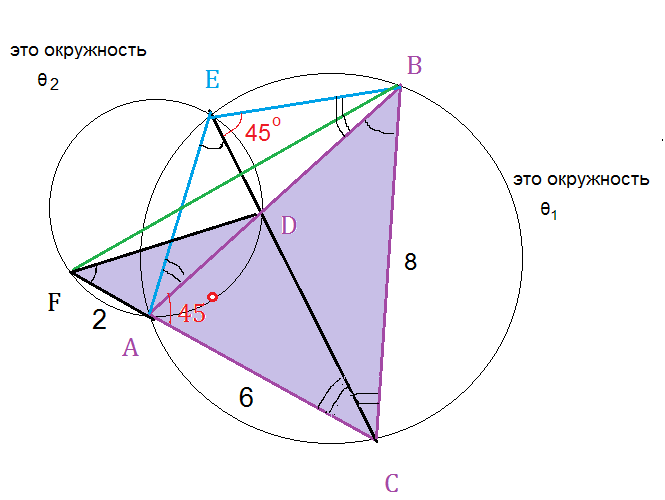
А) Докажите, что центр окружности θ_(1) лежит на прямой FB.

Б) Найдите радиус окружности θ_(2), если известно, что АС=6, AF=2.

SOVA

30.10.2016

★

А) какая-то неясность с центрами и окружностями.

Центр окружности θ_(2) наверное, лежит на прямой FB.

Б)∠AСD=∠DCB - биссектриса СD делит угол пополам.
∠AВС=∠AED как вписанные углы, опирающиеся на дугу АС окружности θ _(1);
∠AED=∠AFD как вписанные углы, опирающиеся на дугу АD окружности θ _(2).

Значит, ∠AFD=∠AВС.
Δ СВF и ΔСBD равны по общей стороне СD и двум прилежащим к ней углам ( два угла в треугольниках равны, значит и третьи углы равны).
ВС=FC=FA+AC=2+6=8

По теореме синусов из треугольника АВС:
ВС/sin ∠ВАС = 2R

R=8/sqrt(2)/2=8/sqrt(2)=4sqrt(2)

[b]R_( θ _(1))=4sqrt(2)[/b]

По теореме косинусов из Δ АВС:
BC^2=AB^2+AC^2-2AB*AC*cos45 °
8^2=AB^2+6^2-2*6*AB*sqrt(2)/2 ⇒ AB^2-6sqrt(2)*AB-28=0 ⇒

D=(6*sqrt(2))^2-4*(-28)=72+112=184=4*46

По свойству биссектрисы СD треугольника АВС:
AD:DB=АС:СВ=6:8 ⇒ [b]AD:DB=3:4[/b] и AD=(3/4)BD