Задача 11 Решить уравнения...

slava191

17.11.2013

Решить уравнения 2sin^2x-5sinxcosx+2cos^2x=0
Выбрать корни принадлежащие [Pi/2;3Pi/2]

Преобразовать, сделать замену.

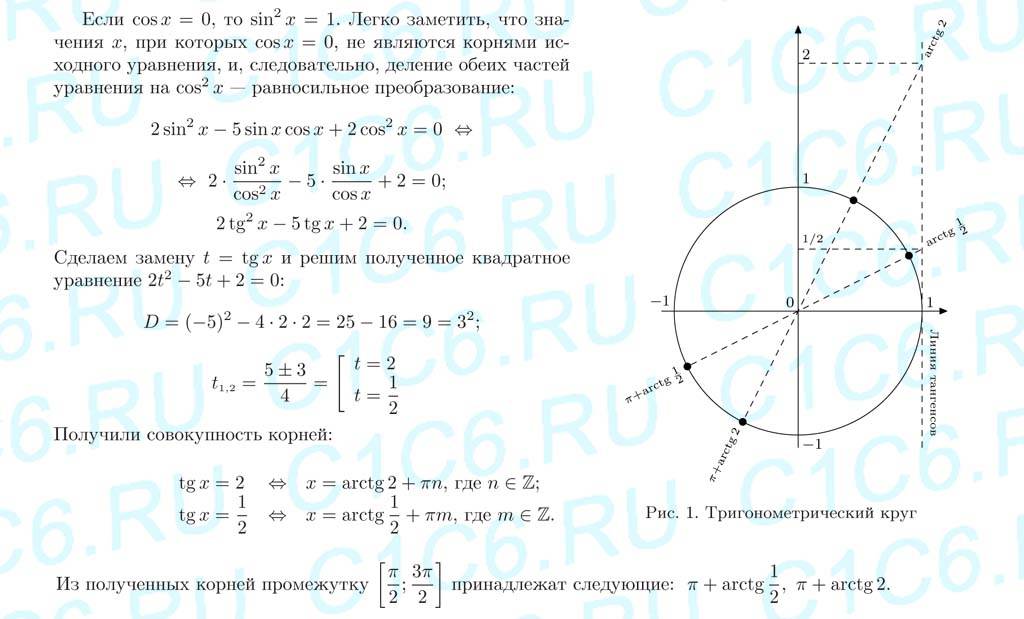
Ответ: a) arctg(1/2)+Pi*n, arctg2+Pi*n б)PI+arctg(1/2), Pi+arctg2

50043172

05.04.2015

делим всё уравнение на cos(x)^2. Получаем: 2tg(x)^2-5tg(x)+2=0, причём cos(x) не равен нулю.
делаем замену t=tg(x) => 2t^2-5t+2=0
Дискриминант: 25-16=9=3^2 => t1=2;t2=0.5;
tg(x)=2 tg(x)=0.5
x=arctg2 +- Pi*n x=arctg0.5 +- Pi*n