Задача 10958 Решите неравенство: log3(x-1)^36 +...
Условие
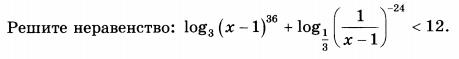
математика 10-11 класс
10680
Решение
★
По формуле перехода к другому основанию
log_(1/3)t=-log_(3)t, t > 0.
Перепишем уравнение в виде:
log_(3)(x–1)^(36) - log_(3)(x–1)^(24) < 12;
log_(3)(x-1)^(12) < log_(3)3^(12)
Логарифмическая функция с основанием 3 > 1 возрастающая, большему значению функции соответствует большее значение аргумента
(x-1)^(12) < 3^(12)
|x-1| < 3
или
-3 < x-1 < 3
-2 < x < 4
C учетом ОДЗ, получаем ответ.
О т в е т. (-2;1)U(1;4).