Задача 10916 а) Решите уравнение 1/sin^2x-1-ctgx=0 б)...
Условие
б) Найдите все корни этого уравнения, принадлежащие промежутку [-Pi/2; Pi/2]
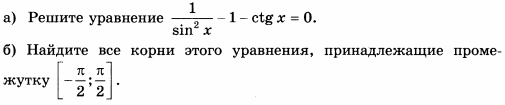
математика 10-11 класс
16469
Решение
★
Уравнение примет вид
(1/sin^2x)-1-(cosx/sinx)=0.
Приводим к общему знаменателю
(1-sin^2x-cosx•sinx)/sin^2x=0
Дробь равна 0 тогда и только тогда когда числитель равен 0, а знаменатель отличен от 0.
Система
{1-sin^2x-cosx•sinx=0
{sin^2x≠0
Так как 1-sin^2x=cos^2x, то первое уравнение перепишется так:
cos^2x-cosx•sinx=0
cosx(cosx-sinx)=0
cosx=0 или сosx-sinx=0
x=(π/2)+πk, k∈ Z или tg x=1
x=(π/4)+πn, n∈ Z
Учитывая sinx≠0 x≠πm, m∈ Z
получаем ответ.
О т в е т. x=(π/2)+πk, x=(π/4)+πn, k,n∈ Z
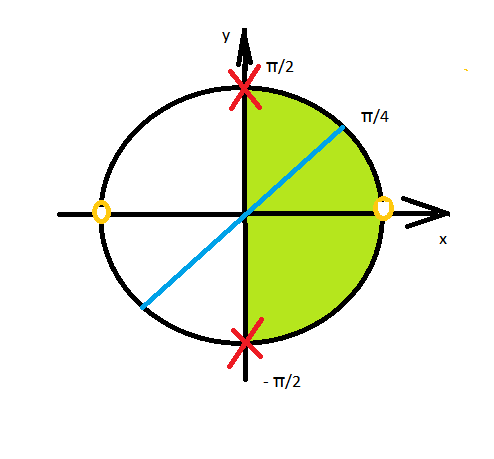
б) Указанному промежутку принадлежат корни:
х=-(π/2); х=(π/4); х=(π/2)