Задача 10833 Решите неравенство:...
Условие
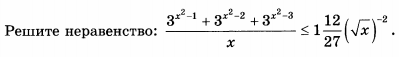
математика 10-11 класс
8078
Решение
★
(√x)^(–2)=1/(√x)^2=1/x при х > 0
3^(x^2–3)• (3^2+3+1)/x ≤ 39/27x;
3^(x^2–3)/x ≤ 3/(27x);
Так как х > 0, то
3^(x^2–3)≤ 1/9;
3^(x^2–3)≤ 3^(–2);
x^2–3 ≤ –2;
x^2–1 ≤ 0;
(x–1)(x+1)≤ 0;
x∈[–1;1]
C учетом ОДЗ
О т в е т. x∈(0;1]