Задача 10795 Решите неравенство:...
Условие
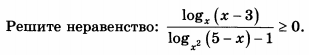
Решение
{x-3 > 0
{5-x > 0
{x > 0; x≠1
{log_(x^2)(5-x)-1≠0
x∈(3;5)
Дробь положительна, когда числитель и знаменатель имеют одинаковые знаки.
Получаем две системы
1){log_x(x-3) больше или равно 0
{log_(x^2)(5-x)-1 > 0
2){log_x(x-3) меньше или равно 0
{log_(x^2)(5-x)-1 < 0
Решаем первую систему.
Так как согласно ОДЗ х∈(3;5), логарифмическая
функция возрастающая и большему значению функции соответствует большее значение аргумента
{x-3≥1
{5-x > x^2
{x≥4
{x^2+x-5 < 0 D=1+20=21
корни (-1±sqrt(21))/2
система не имеет решений. (-1+sqrt(21))/2 < 4
Решаем вторую систему
{x-3≤1
{5-x < x^2
{x≤4
{x^2+x-5 > 0 D=1+20=21
корни (-1±sqrt(21))/2
x∈ (-∞;-1-sqrt(21))/2)U(-1+sqrt(21))/2;4]
C учетом ОДЗ получаем ответ.
х∈(3;4]
О т в е т. (3;4]