Задача 10792 а) Решите уравнение tgx+ctgx=2. б)...
Условие
б) Найдите все корни этого уравнения, принадлежащие промежутку [Pi; 3Pi].
математика 10-11 класс
18308
Решение
★
ctgx=cosx/sinx; x≠ πn, n ∈ Z
(sin^2x+cos^x)/(sinxcosx)=2
Так как sin^2x+cos^x=1, то
1/(sinxcosx)=2
или
sinxcosx=1/2
Применяем формулу синуса двойного угла:
sin2x=2sinxcosx
Уравнение принимает вид
sin2x=1
2x=(π/2)+2πm, m∈Z
x=( π/4)+πm, m∈Z
а) О т в е т. x=(π/4)+πm, m∈Z
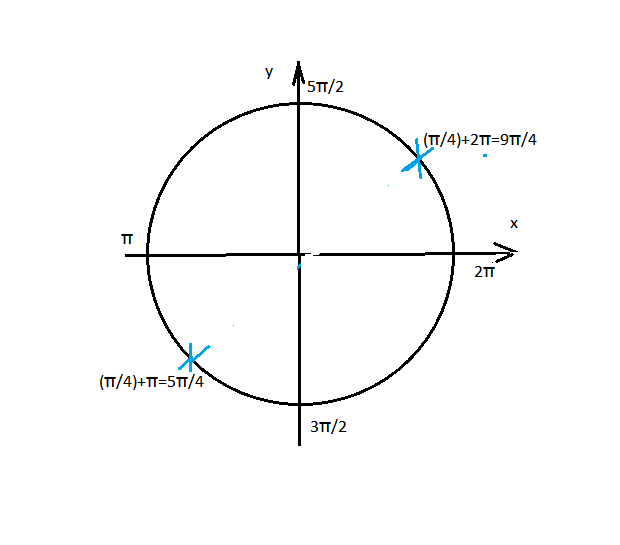
б) Указанному промежутку принадлежат
корни 5π/4 и 9π/4.
см рисунок.
О т в е т. б) 5π/4 и 9π/4