Задача 10783 Найдите все значения параметра а, при...
Условие
Решение
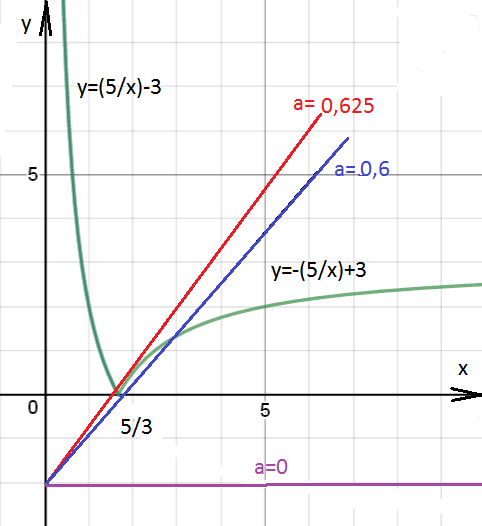
y=2ax–2 – задает прямую. При a=0 прямая y=–2 параллельна оси Ох и не имеет общих точек с графиком.
Исключим те значения параметра а, при которых прямая имеет более одной точки пересечения с графиком.
Одна такая прямая проходит через точку (5/3) на оси Ох
Подставляем координаты это точки в уравнение прямой и находим граничное значение а.
0=2а•(5/3)–2 ⇒ а=0,6
Прямые имеющие коэффициент а несколько больше чем 0,6 будут иметь две точки пересечения с графиком.
До какого значения а это будет продолжаться?
Найдем это граничное значение а, при котором прямая у=2ах–2 является касательной к кривой у=(–5/х)+3.
Напишем уравнение касательной к кривой у=(–5/x+3), в точке х0=c, которая проходит через точку (0;–2)
f`(x)=5/x2
f`(c))=5/c2
y–((–5/c) +3)=(5/c2)•(x–c)
Так как точка (0;–2) принадлежит касательной
–2+(5/с)–3=(5/с2)•(–c)⇒ c=2
f(2)=(–5/2)+3=1/2
Прямая у=2ax–2 проходит через точку (2;1/2)
найдем при каком а
1/2=2a•2–2
a=0,625
О т в е т. а∈(0;0,6)U(0,625;+∞)