Задача 10781 Решите неравенство...
Условие
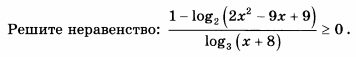
Решение
{2x^2-9x+9 > 0 D=81-4•2•9=81-72=9 Корни 1,5 и 3
{x+8 > 0
x∈(-8;1,5)U(3;+∞)
Дробь положительна, тогда и только тогда когда числитель и знаменатель имеют одинаковые знаки.
Дробь равна 0 тогда и только тогда, когда числитель равен 0, а знаменатель отличен от нуля.
Получаем две системы
1)
{1-log_(2)(2x^2-9x+9) меньше или равно 0;
{log_(3)(x+8) < 0
или
2){1-log_(2)(2x^2-9x+9) больше или равно 0;
{log_(3)(x+8) > 0
Решаем первую
1){log_(2)(2x^2-9x+9) больше или равно log_(2)2;
{log_(3)(x+8) < log_(3)1.
{2x^2-9x+9 больше или равно 2;
{x < 1 - 8.
{2x^2-9x+7 больше или равно 0;D=81-56=25 корни 1 и3,5
{x < -7.
x∈(-∞;-7)
С учетом ОДЗ:
(-8;-7)
Решаем вторую
2){log_(2)(2x^2-9x+9) меньше или равно log_(2)2;
{log_(3)(x+8) > log_(3)1.
{2x^2-9x+9 меньше или равно 2;
{x+8 > 1.
{2x^2-9x+7 меньше или равно 0;D=81-56=25,корни 1 и3,5
{x > 1-8.
x∈[1;3,5]
С учетом ОДЗ:
x∈[1;1,5)U(3;3,5]
О т в е т. x∈(-8;-7)U[1;1,5)U(3;3,5]