Задача 10762 ...

slava191

23.10.2016

Окружность ω с центром в точке О касается стороны BC треугольника ABC в точке M и продолжений сторон AB и AC. Вписанная в этот треугольник окружность с центром в точке Е касается стороны BC в точке K.

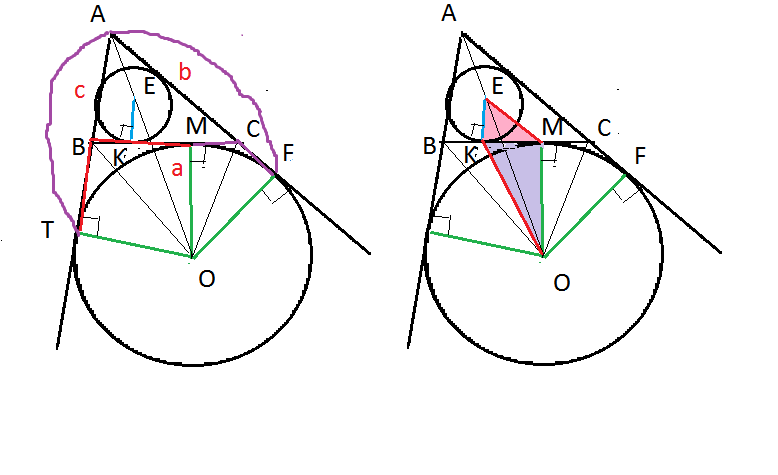
а) Докажите, что ВК=СМ.

б) Найдите площадь четырехугольника ОКЕМ, если известно, что АС=5, ВС=6, АВ=4.

SOVA

26.10.2016

★

Пусть АВ=с; BC=a; AC=b
Окружность ω является вневписанной окружностью.
Поэтому при решении задачи нужны некоторые свойства этой окружности.
Центр О этой окружности - точка пересечения биссектрис внешних углов B и С треугольника АВС.
По свойству касательной к окружности
ВТ=ВМ; СМ=CF; AT=AF
и AL=AD; BL=BK; CK=CD
Р( Δ АВС)=a+b+c= AB+BM+MC+AC= AB+BT+AC+CF=AT+AF=2AF⇒
AF=AT=P/2=p
Тогда BT=BM=p-c; CM=CF=p-b
AL=AD=p-a, так как
AL+LB+BK+KC+CD+AD=P, то
AL+AD+(BK+BK+KC+KC)=P;
2AL+2a=P ⇒ AL=p-a

Тогда ВК=ВL=AB-AL=c-(p-a)=a+c-p и
СM=BC-BM=a-BT=a-(p-c)=a+c-p
Откуда ВК=СМ.
Можно найти
КМ=BM-BK=BT-BK=(p-c)-(a+c-p)=2p-2c-a=b-c.
Известна формула нахождения радиуса вневписанной окружности ( находится методом площадей)
OT=OM=OF=S(Δ АВС)/(p-a)

OE=S/p

S(Δ АВС)=sqrt(7,5•(7,5-6)•(7,5-5)•(7,5-4))=
=15sqrt(7)/4

OT=OM=OF=(15sqrt(7)/4):(7,5-6)=5sqrt(7)/4

OE=OK=OD=(15sqrt(7)/4):7,5=sqrt(7)/2

S(OKEM)= S(Δ EKM) + S(ΔKMO)= (KM•EK/2)+(KM•OK/2)=
=(KM/2)•(EK+OK)=((5-4)/2)(5sqrt(7)/2+sqrt(7)/2)=
=3sqrt(7)/2.