Задача 1074 Стартуя из точки А (см. рисунок),...
Условие
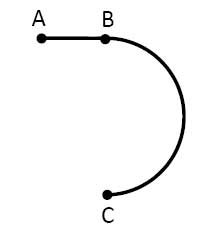
физика 10-11 класс
76235
Решение

Ответ: Pi
Обсуждения


Ответ: Pi