Задача 10708 Найдите все значения а, при каждом из...
Условие
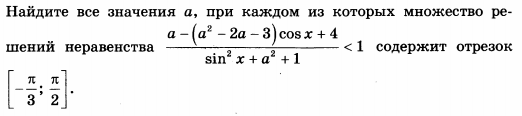
Решение
Неравенство примет вид:
a-(a^2-2a-3)cosx+4 < sin^2x+a^2+1.
sin^2x=1-cos^2x;
cos^2x-(a^2-2a-3)cosx+2+a-a^2 < 0
На [-π/3; π/2] множество значений функции у=cosx равно [0;1].
Обозначим сosx=t.
Переформулируем задачу.
Найти все значения параметра а, при каждом из которых t^2-(a^2-2a-3)t+2+a-a^2 < 0 при всех t∈[0;1]
Для выполнения этого необходимо и достаточно, чтобы квадратичная функция f(t)=t^2-(a^2-2a-3)t+2+a-a^2 , графиком которой является парабола, ветви направлены вверх, была расположена ниже оси оси на [0;1].
Это условие принимает вид
{f(0) < 0
{f(1) < 0
Тогда для всех точек t∈[0;1]
будет выполняться неравенство: f(t) < 0
[a^2+a+2 < 0;
{-2a^2+3a+6 < 0
или
{a^2-a-2 > 0; D=1+8=9 корни -1 и 2
{2a^2-3a-6 > 0 D=9-4•2•(-6)=9+48=57
корни (3-√57)/4 и (3+√57)/4
___((3-√57)/4)___(-1)_____(2)_____((3-√57)/4)
О т в е т. (-∞; (3-√57)/4)U((3+√57)/4;+∞)