Задача 10702 Найти все значения параметра а, при...
Условие
|5^(x+1)-a|-|5^x+2a|=25^x имеет ровно два неотрицательных решения.
Решение
5^x=t > 0; 25^x=(5^2)^x=(5^x)^2=t^2
Если 5^x=t_(1) или 5^x=t_(2)
t_(1) больше или равно 1 и t_(2) больше или равно 1, то данное уравнение будет иметь два неотрицательных корня.
После введённой замены
уравнение примет вид
|5t–a|–|t+2a|=t^2.
Применяем координатно–параметрический метод.
Рассматриваем плоскость аОt
Раскрываем знак модуля в каждой из четырех областей.
1) Подмодульные выражения обращаются в 0
при 5t–a=0 ⇒ t=a/5
при t+2a=0 ⇒ t=–2a
Прямые t=a/5 и t=–2a разбивают координатную плоскость аОt на 4 области.
Раскрываем знаки модуля в каждой области
1 область
{5t-a больше или равно 0
{t+2a больше или равно 0
5t–a-t+2a=t^2 ⇒ a=(-1/3)(t^2-t) - зеленая парабола
Вершина параболы в точке t=1/2 a=1/8.
О т в е т. два неотрицательных решения 0 < t меньше или равно 1 при 0 < a меньше или равно 1/8
Обратная замена приводит к уравнениям
5^x=t_(1) или 5^(x)=t_(2),
не имееющим неотрицательных решений.
В первой области нет решений.
2 область
{2t-a больше или равно 0
{t+2a < 0
2t–a+t+2a=t^2 ⇒ a=t^2–3t
парабола оранжевого цвета, оставлена только та её часть, которая принадлежит области 2.
Вершина в точке t=1,5; a=–2,25.
На (-2,25;-2]
Уравнение имеет два решения
t от 1 до 2
Обратная замена
приводит к двум уравнениям
5^x=t_(1) или 5^(x)=t_(2)
Решение которых и дает неотрицательных решения х
3 область
и
4 область
расположены ниже оси Оа
положительных значений t нет, а значит и уравнение
5^x=t не будет иметь решений
Поскольку показательное уравнение
5^x=t имеет положительный корень, если t > 1, то
при a∈(–2,25;–2] данное уравнение будет иметь ровно два неотрицательных корня.
О т в е т. a∈(–2,25;–2]
Уравнение примет вид
|5t–a|–|t+2a|=t^2.
Применяем координатно–параметрический метод.
Раскрываем модули.
1) Подмодульные выражения обращаются в 0
при 5t–a=0 ⇒ t=a/5
при t+2a=0 ⇒ t=–2a
Прямые t=a/5 и t=–2a разбивают координатную плоскость аОt на 4 области.
Раскрываем знаки модуля в каждой области
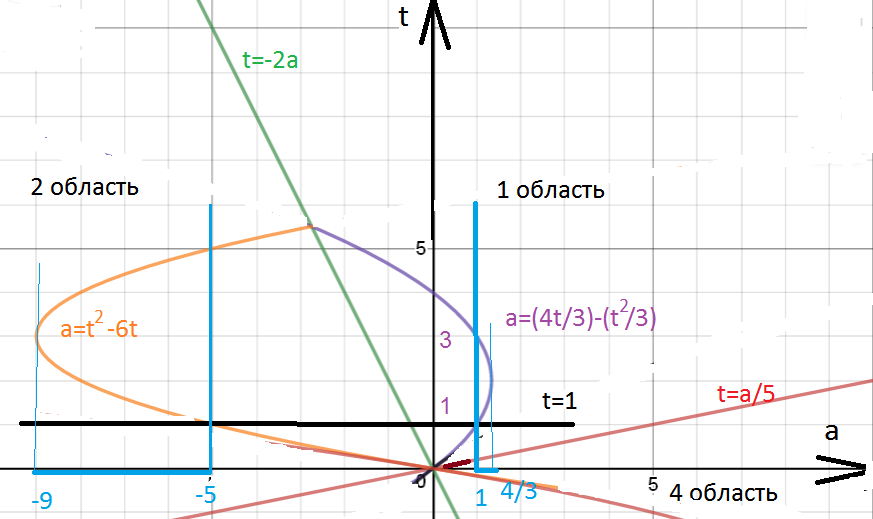
1 область
5t–a–t–2a=t^2 ⇒ a=(4t–t^2)/3
парабола сиреневого цвета, оставлена только та ее часть, которая расположена в области 1.
Вершина параболы в точке t=2 a=4/3.
Поскольку показательное уравнение
5^x=t имеет положительный корень, если t > 1, то
при a∈U[1;4/3) данное уравнение будет иметь ровно два неотрицательных корня.
2 область
5t–a+t+2a=t^2 ⇒ a=t^2–6t
парабола оранжевого цвета, оставлена только та её часть, которая принадлежит области 2.
Вершина в точке t=3; a=–9.
3 область
и
4 область
расположены ниже оси Оа и дают отрицательные значения t
Поскольку показательное уравнение
5^x=t
при t меньше или равно 0 не имеет решений вообще.
при a∈(–9;–5] уравнение будет иметь ровно два неотрицательных корня.
О т в е т. a∈(–9;–5]U[1;4/3)
Ответ: a∈(–9;–5]U[1;4/3)
Все решения