Задача 10648 Ребро SA пирамиды SABC перпендикулярно...

slava191

19.10.2016

Ребро SA пирамиды SABC перпендикулярно плоскости основания АВС.

а) Докажите, что высота пирамиды проведённая из точки А, делится плоскостью, проходящей через середины рёбер АВ, АС и SA, пополам.

б) Найдите расстояние от вершины А до этой плоскости, если SA = sqrt(5) , АВ = АС = 5, ВС = 2sqrt(5).

SOVA

19.10.2016

★

а)Пусть М- середина ребра SA, К-середина ребра АС, Т-середина ребра АВ.
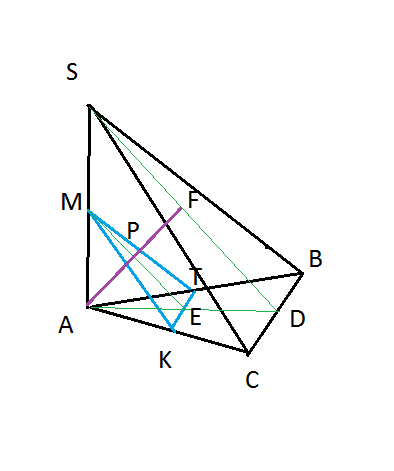
Тогда МК- средняя линия треугольника SAC, MT- средняя линия треугольника SAB, КТ- средняя линия треугольника ABС.
Так как треугольник SCB- равнобедренный (АС=АВ, равные проекции имеют равные наклонные), то высота пирамиды, проведенная из точки А проектируется на высоту равнобедренного треугольника SBC.
Пусть SD- высота треугольника SBC, AD- высота треугольника АВС.
Треугольники SAF и MAР подобны с коэффициентом подобия 2, значит плоскость МКТ делит высоту AF пополам.
б) Из прямоугольного треугольника SAD:
SA•AD/2=AF•SD/2
По теореме Пифагора
АD^2=AC^2-CD^2=5^2-(√5)^2=25-5=20
AD=2√5
По теореме Пифагора
SD^2=SA^2+AD^2=(√5)^2+(2√5)^2=5+20=25.

√5•(2√5)/2=AF•5/2
AF=2
АР=AF/2=1
О т в е т. AP=1