Задача 1063 За цикл, показанный на рисунке, газ...
Условие
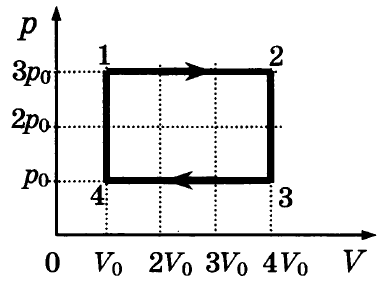
физика 10-11 класс
82627
Решение
Полезная работа цикла равна площади, ограниченной графиком цикла: Aц=6*Po*Vo; Сравнивая эти выражения, получим A=9/6*Aц.
С другой стороны, полезную работу можно вычислить через КПД : Aц=4/17*Q=4/17*5,1 кДж=1,2 кДж.
Работа на участке 1-2 A=9/6*1,2 кДж=1,8 кДж.
Ответ: 1,8 кДж