Задача 10616 Дано уравнение (cos2x+cosx+1)/(sinx-1) =...

slava191

17.10.2016

Дано уравнение (cos2x+cosx+1)/(sinx-1) = 0

А) Решите уравнение.
Б) Укажите корни уравнения, принадлежащие отрезку [-9Pi/2; -3Pi]

SOVA

17.10.2016

★

А) Дробь равна 0 тогда и только тогда, когда числитель равен 0, а знаменатель отличен от 0.
Система
{cos2x+cosx+1=0,
{sinx–1 ≠ 0; х ≠(π/2)+2πm, m∈Z


cos2x=2cos^2x-1, поэтому первое уравнение принимает вид
2cos^2x-1+сosx+1=0
2cos^2x+cosx=0
cosx(2cosx+1)=0
cosx=0 или 2 сosx+1=0
x=(π/2)+πk, k∈Z
или
cosx=-1/2
x=±arccos(-1/2)+2πn, n ∈ Z.
x=±(π-arccos(1/2))+2πn, n ∈ Z.
x=±(π-(π/3))+2πn, n ∈ Z.
x=±(2π/3)+2πn, n ∈ Z.
О т в е т.
А) x=(-π/2)+2πk, x=±(2π/3)+2πn, k, n ∈ Z.

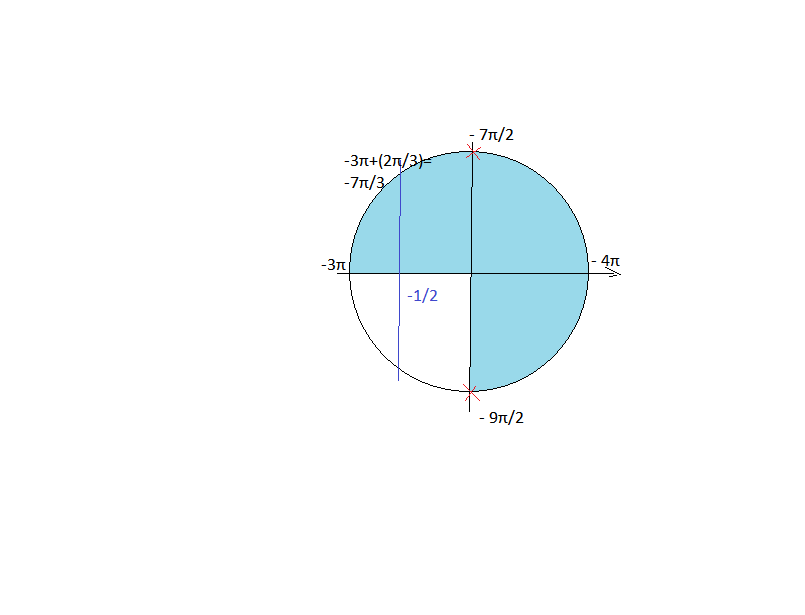
Б) Указанному промежутку принадлежат корни
(см. рисунок)
-7π/3; -9π/2