Задача 1060 На плоскую непрозрачную пластину с...

slava191

02.05.2014

На плоскую непрозрачную пластину с узкими параллельными щелями падает по нормали плоская монохроматическая волна из красной части видимого спектра. За пластиной на параллельном ей экране наблюдается интерференционная картина, содержащая большое число полос. При переходе на монохроматический свет из синей части спектра:
1. Расстояние между интерференционными полосами уменьшатся;
2. Интерференционная картина станет невидимой для глаза;
3. Расстояние между полосами не изменятся;
4. Расстояние между полосами увеличится?

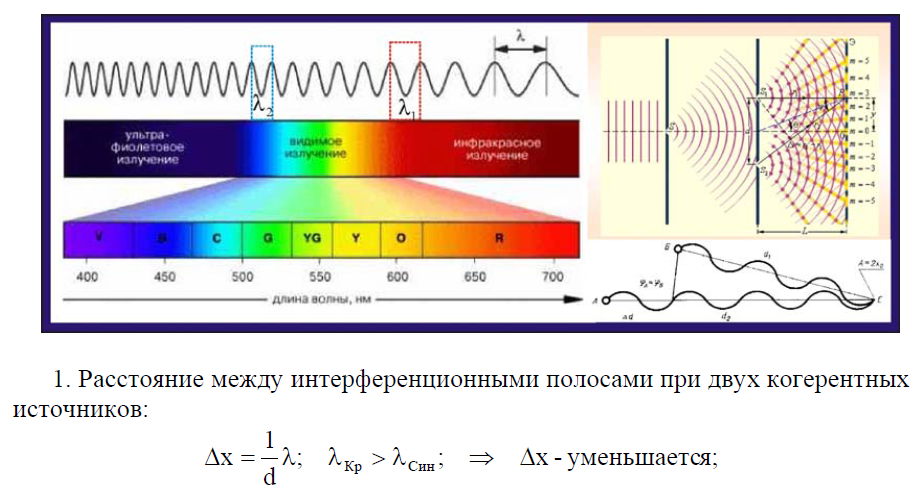
Ответ: Расстояние между интерференционными полосами уменьшатся