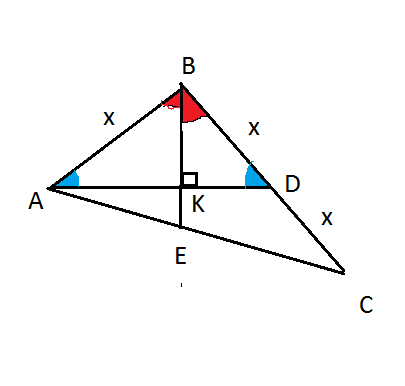
Задача 10592 В треугольнике ABC биссектриса BE и...

slava191

16.10.2016

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 168. Найдите стороны треугольника ABC.

SOVA

16.10.2016

★

Прямоугольные треугольники АВК и ВКD равны по общему катету ВК и острому углу.
∠АВЕ=∠ЕВС
Тогда треугольник АВD- равнобедренный.
Пусть АВ=х, тогда ВD=x, DC=BD=x и значит ВС=2х.
Пусть ∠АВЕ=∠ЕВС=α.
Тогда
KD=BD•sinα=x•sinα
AD=2KD=2x•sinα
168=2x•sinα
sinα=84/x

Известна формула вычисления биссектрисы угла между двумя сторонами
ВЕ=2•х•(2х)•сosα/(x+2x);
168=4xcosα/3
cosα=126/x

Так как sin^2α+cos^2α=1, то
(84/x)^2+(126/x)^2=1⇒ x^2=(84^2+126^2)
x=√(7056+15876)=42√13
АВ=42√13
ВС=84√13

cosα=126/x=126/42√13=3/√13
cos2α=2cos^2α-1=2•(3/√13)^2-1=5/13

По теореме косинусов из треугольника АВС
АС^2=x^2+(2x)^2-2•x•(2x)•(5/13)
АС^2=5x^2-4x^2•(5/13)
AC^2=5•(42√13)^2-4(42√13)^2•(5/13)
AC^2=5•(42√13)^2(1-(4/13))
АС=42√13•3√5/√13=126√5.
О т в е т. 42√13; 84√13; 126√5.