Задача 10559 Решить 8sin^2x+2sqrt(3)cos(3Pi/2-x) = 9...
Условие
математика 10-11 класс
26701
Решение
★
cos(3π/2–x)=-sinx,
уравнение принимает вид
8sin^2x-2√3sinx-9=0
D=(-2√3)^2-4•8•(-9)=12+288=300
√D=10√3
sinx=[m]\frac{2√3-10√3}{16}[/m]
sinx=-[m]\frac{√3}{2}[/m]
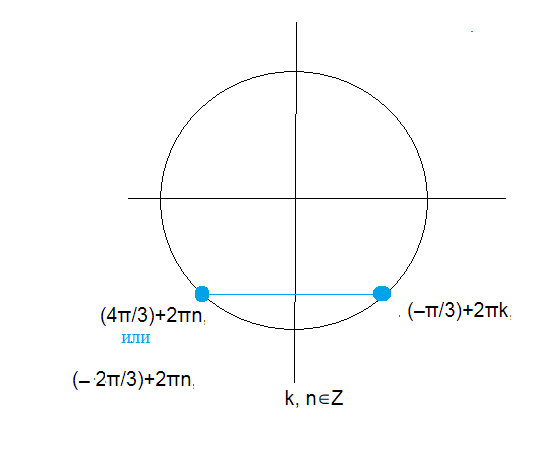
x=(-π/3)+2πk, k∈Z или х=(π-(-π/3))+2πn, n∈Z
x=(-π/3)+2πk, k∈Z или х=4π/3)+2πn, n∈Z
ИЛИ
sinx=[m]\frac{2√3+10√3}{16}[/m]
sinx=[m]\frac{3√3}{4}[/m]
уравнение не имеет корней, |[m]\frac{3√3}{4}[/m]| > 1
О т в е т. (-π/3)+2πk, (4π/3)+2πn, k, n∈Z