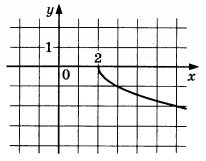
Задача 10537 На рисунке изображён график функции у =...

slava191

14 октября 2016 г.

На рисунке изображён график функции у = f(x). Прямая, проходящая через точку (–1; 1), касается этого графика в точке с абсциссой 3. Найдите f'(3).

SOVA

14 октября 2016 г.

★

Геометрический смысл производной в точке:
f`(x₀)=k(касательной)
Касательная к кривой проходит через точку с абсциссой х₀
Напишем уравнение касательной в виде
у=kx+b.
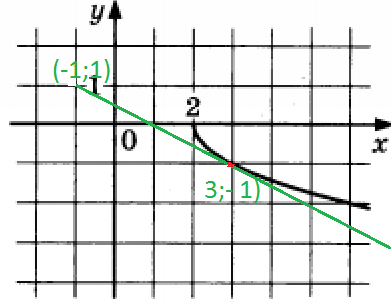
Чтобы найти k подставим координаты точек (–1;1) и (3;–1)
1=k•(–1)+b
–1=k•3+b
Получаем систему двух уравнений
{1=k•(–1)+b;
{–1=k•3+b
Вычитаем из первого уравнения второе
1–(–1)=–k–3k;
2=–4k;
k=–1/2
k(касательной)=–1/2.

Можно написать уравнение касательной как уравнение прямой, проходящей через две точки (–1;1) и (3;–1).
Уравнение прямой проходящей через две точки с координатами (х₁;у₁) и (х₂;у₂) имеет вид
(x–x₁)/(x₂–x₁)=(y–y₁)/(y₂–y₁).
(х–(–1))/(3–(–1))=(у–1)/(–1–1)
(х+1)/4=(у–1)/(–2)
Пропорция, умножаем крайние и средние члены пропорции:
–2(х+1)=4(y–1)
4y+2x–2=0
y=(–1/2)x+(1/2)
k(касательной)=–1/2

Значит, f`(3)=–1/2

О т в е т. f`(3)=–1/2