Задача 10468 Решите неравенство...
Условие
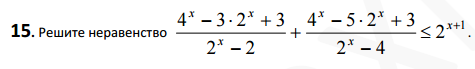
математика 10-11 класс
6508
Решение
★
2^x≠4 ⇒ x≠2
x∈(-∞;1)U(1;2)U(2;+∞)
Замена переменной
2^x=t;
t > 0
4^x=(2^2)^x=(2^x)^2=t^2
2^(x+1)=2•2^x=2t
Неравенство примет вид:
(t^2-3t+3)/(t-2) + (t^2-5t+3)/(t-4) меньше или равно 2t;
переносим 2t влево и приводим дроби к общему знаменателю:
-2(t^2-6t+9)/(t-2)(t-4) меньше или равно 0
или
(t-3)^2/(t-2)(t-4) больше или равно 0
(t-3)^2 > 0 при любом t;
(t-3)^2=0 при t=3 ⇒
(t-2)(t-4) > 0
t=3
_+__(2)__[3]__(4)_+__
C учетом t > 0
(0;2)U{3}U(4;+∞)
Обратная замена
0 < 2^x < 2⇒ x < 1
2^x=3 ⇒ x=log_(2)3
2^x > 4 ⇒ x > 2
О т в е т. (- бесконечность;1)U{log_(2)3}U(2;+бесконечность)