Задача 1034 Высота SO правильной треугольной...
Условие
математика 10-11 класс
14578
Решение
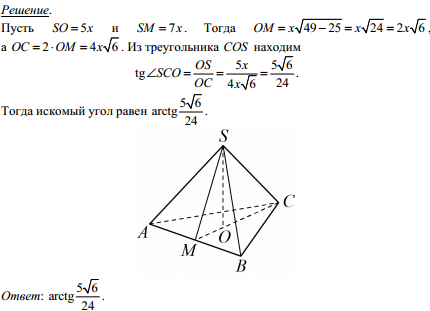
Ответ: В решение

Ответ: В решение