Задача 10297 Решите неравенство...
Условие
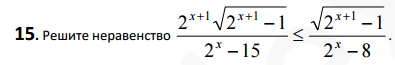
математика 10-11 класс
5041
Решение
★
2^x=t
Неравенство примет вид:
2t√(2t-1)/(t-15) меньше или равно √(2t-1)/(t-8)
или
(2t^2-16t-t+15)√(2t-1)/(t-15)(t-8) меньше или равно 0;
(t-1)(2t-15)√(2t-1)/(t-15)(t-8) меньше или равно 0.
ОДЗ: 2t-1 больше или равно 0.
Решаем методом интервалов на [1/2; + бесконечность)
[1/2] _+_ [1] __-__[15/2] _+_ (8) __-___ (15)___+__
t=(1/2) или 1 меньше или равно t меньше или равно (15/2)
или 8 < t < 15.
Обратная замена
2^x=2^(-1) или 2^(0) меньше или равно 2^x меньше или равно 2^(log_(2)15/2)
или 2^3 < 2^x < 2^(log_(2)15).
О т в е т. {-1} U [0; log_(2)15/2]; (3; log_(2)15)