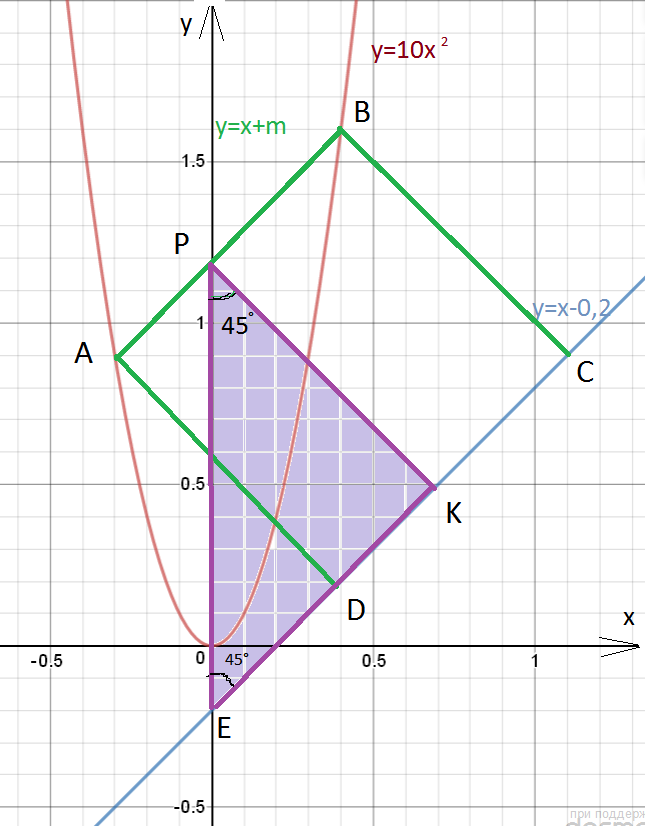
Задача 10288 Даны парабола y=10x^2 и прямая y=x-0.2 ....
Условие
Решение
Пусть точки А(х_(А);у_(А)) и В(х_(В);у_(В)) лежат на параболе, а точки С и D на прямой у=х-0,2.
Противоположные стороны квадрата параллельны.Значит,
точки А и В лежат на прямой АВ, параллельной прямой у=х-0,2.
Пусть это прямая у=х+m.
Значит, у_(А)=х_(А)+m; y_(B)=x_(B)+m
Расстояние между точками А и В
d^2=(x_(B)-x_(A))^2+(y_(B)-y_(A))^2=
= (x_(B)-x_(A))^2+(x_(B)-m-y_(A)+m)^2=
=2• (x_(B)-x_(A))^2.
Рассмотрим прямоугольный треугольник РКЕ, PK⊥CD.
Р-точка пересечения прямой у=х+m c осью ОУ.
Р(0;m)
Е- точка пересечения прямой у=х-0,2 с осью ОУ.
Е(0;-0,2)
РЕ=m+0,2
Прямые у=х+m и у=х-0,2 образуют с осью Ох угол 45°, а значит и с осью Оу - 45°.
РК=ВС=d=(m+0,2)•sin45°=(m+0,2)/√2.
d^2=(m+0,2)^2/2.
Все стороны квадрата равны.
АВ=ВС, но ВС=РК, значит
AB=PK. Получаем уравнение
(m+0,2)^2/2=2•(x_(B)-x_(A))^2.
-----------------------------
Так как точки А и В лежат на параболе, то
у_(А)=10х^2_(А); у_(В)=10х^2_(В)
и на прямой, то
m=10х^2_(B)-x_(B)=10х^2_(А)-х_(А) или
10х^2_(А)-х_(А)=10х^2_(B)-x_(B).
Откуда х_(А)+х_(В)=0,1.
-------------
4•(2х_(В)-0,1)^2=(10x^2_(B)-x_(B)+0,2)^2
Упрощаем
100х^4_(B)-20x^3_(B)-11x^2_(B)+1,2x_(B)=0
(x_(B)-0,1)(10x_(B)-4)(10x_(B)+3)=0
при x_(B)=0,4 и х=-0,3 получим наибольшее значение
d^2=2•(2х_(В)-0,1)^2=2•(2•0,4-0,1)^2=2•0,7^2=0,98
d^2=2•(2х_(В)-0,1)^2=
=2•(2•(-0,3)-0,1)^2=2•(-0,7)^2=0,98
S=d^2=0,98.