Задача 10272 ...

vk305743633

30.09.2016

a) Решите уравнение 4sin^42x+3cos4x–1=0
б) Отберите корни на промежутке [π; 3π/2]

SOVA

30.09.2016

★

а)
4sin^42x + 3cos4x – 1 =0;
4•((1 – cos4x)/2)^2 + 3cos4x – 1 = 0;
cos^24x + cos4x =0;
cos4x(cos4x + 1) = 0
cos4x = 0 или сos4x+1=0
4x= (π/2)+ πk, k∈Z или сos4x=-1
4x= π + 2πn, n∈Z
x= (π/8)+ (π/4)k, k∈Z или х=(π/4)+ (π/2)n, n∈Z

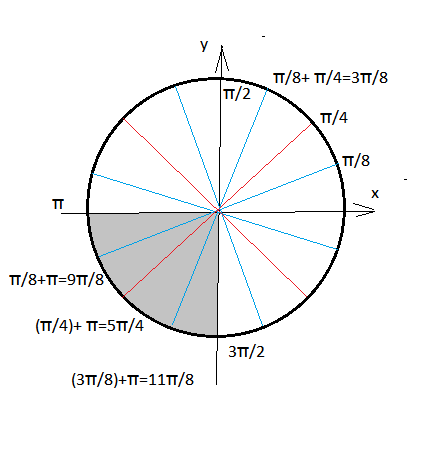
б)
Отбор корней см на рисунке.
О т в е т. 9π/8; 5π/4; 11π/8

vk305752838

30.09.2016

4sin^4(2x) + 3cos(4x) - 1 = (1 - cos(4x))^2 + 3cos(4x) - 1 = 1 + cos^2(4x) - 2cos(4x) + 3cos(4x) - 1 = cos^2(4x) + cos(4x) = cos(4x)[cos(4x) + 1] = 0
cos(4x) = 0

4x = +-pi/2 + pik

x1 = +-pi/8 + pik/4

cos(4x) + 1 = 0

cos(4x) = -1

4x = +-pi + pik

x2 = +-pi/4 + pik/4, k E Z