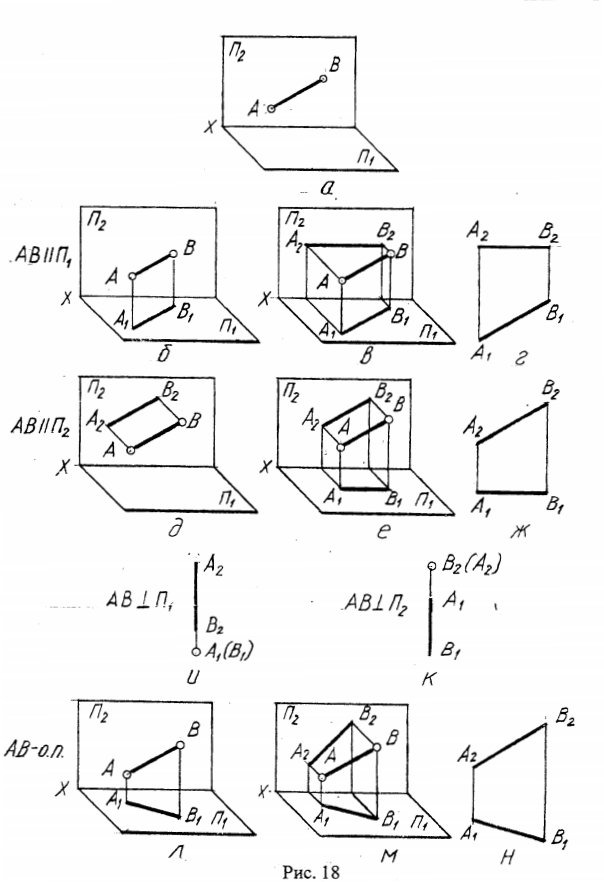
Перебросим логический мостик от пункта 1 к пункту 2. Посмотрите на эпюры отрезков разного положения /рис.18г,ж,и,к,м/. Подумайте, есть ли среди проекций отрезков АВ такие, которые имеют натуральную длину его самого? Вспомним, что отрезок, параллельный плоскости проекций, проецируется на нее без искажений. Так и было в случаях г(A1B1=AB) и ж(А2В2=АВ). Но если отрезок перпендикулярен одной из плоскостей проекций, то другой он параллелен, поэтому в натуральную величину отрезок представлен в случаях и(А2В2=АВ) и k(A1B1=AB). И лишь у отрезка общего положения, наклоненного к обеим плоскостям, каждая проекция короче него самого, а потому на эпюре м натуральной величины отрезка АВ нет. Но ведь это общий, а не частный случай и встречается в практике начертательной геометрии чаще них. Между тем, при решении метрических задач, в которых предусматривается оперирование метрически определенными элементами или их получение, часто требуется найти натуральную величину отрезка по его проекциям. Вот почему задача, к рассмотрению которой мы переходим, является одной из ключевых в предлагаемом курсе.
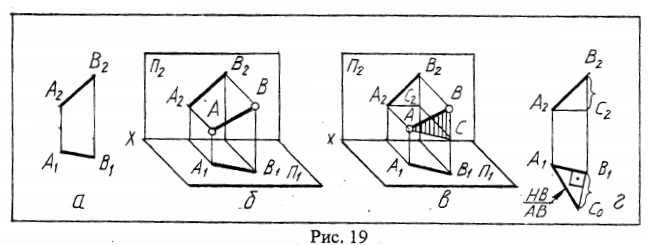
 Задача. Найти натуральную величину (НВ) отрезка АВ по его проекциям /рис. 19а/.
Задача. Найти натуральную величину (НВ) отрезка АВ по его проекциям /рис. 19а/.
Метод вращения
Рассмотрим решение, в котором заданный эпюр используется без предварительных преобразований, т.е. необходимые для решения построения выполняются непосредственно на заданном графическом условии. В данном случае суть этих построений состоит в следующем. Проведем АС || A1B1 /рис.19в/. Треугольник ABC - прямоугольный, т.к. АС || П1, ВС перпендикулярно П1. Найти на эпюре НВ АВ - значит построить гипотенузу АВ треугольника ABC, что легко сделать по двум его катетам. Тогда AC=A1B1 как противоположные стороны прямоугольника ACB1A1, поэтому один из катетов на эпюре уже имеется - это А1В1. Найдя фронтальную проекцию С, соединим С2 и А2. В2С2=ВС, значит В2С2 и есть второй катет. Теперь на эпюре /рис.19г/ проведем А2С2 параллельно П1 и получим В2С2. В заключение проводим через В1 луч, перпендикулярный А|В|, и откладываем на нем В2С2. Соединив точку С0 с А1, получаем А1С0, - искомую натуральную величину отрезка АВ.
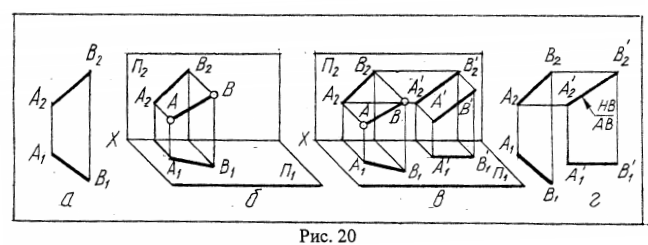
 Вернемся к первоначальному графическому условию /рис.20а,б/ и постараемся решить ту же задачу другим путем. Передвинем ABB1A1 /рис.20в/, не отрывая эту трапецию от П1 так, чтобы после поворота она стала параллельной П2. Теперь отрезок А'В' также параллелен П2, а значит - проецируется на эту плоскость в натуральную величину. Повторим проделанные действия на эпюре /рис.20г/. Поскольку после поворота АВ в положении, параллельное П2, его проекция A1B1 должна расположиться горизонтально, начертим А1'В1', в этом положении. Заметим, что A1'B1' можно расположить правее или левее, выше или ниже выбранного положения, т.к. в любом из этих случаев сам отрезок остается параллельным П2. Восставим линии связи из A1'B1'. Трапеция ABB1A1 передвигалась без отрыва от П1 (такое перемещение в начертательной геометрии называют плоско-параллельным), поэтому в итоге высота точек А' и В' над плоскостью П1 не изменилась. По этой причине линии, соединяющие на рис.20в точки А2 и A2', а также В2 и В2', - есть линии горизонтальные. То же происходит и на эпюре, а значит, для нахождения точек А2'В2' через А2 и В2 достаточно провести горизонтальные линии связи до их пересечения с соответствующими вертикальными линиями связи. А2'В2' - есть искомая натуральная величина отрезка АВ. В рассмотренном случае она получена методом вращения за счет того, что отрезок общего положения АВ был повернут параллельно одной из плоскостей проекций. Итак, сущность метода вращения состоит в том, что при неизменном положении плоскостей проекций изображаемый объект поворачивается в положение, удобное для решения задачи.
Вернемся к первоначальному графическому условию /рис.20а,б/ и постараемся решить ту же задачу другим путем. Передвинем ABB1A1 /рис.20в/, не отрывая эту трапецию от П1 так, чтобы после поворота она стала параллельной П2. Теперь отрезок А'В' также параллелен П2, а значит - проецируется на эту плоскость в натуральную величину. Повторим проделанные действия на эпюре /рис.20г/. Поскольку после поворота АВ в положении, параллельное П2, его проекция A1B1 должна расположиться горизонтально, начертим А1'В1', в этом положении. Заметим, что A1'B1' можно расположить правее или левее, выше или ниже выбранного положения, т.к. в любом из этих случаев сам отрезок остается параллельным П2. Восставим линии связи из A1'B1'. Трапеция ABB1A1 передвигалась без отрыва от П1 (такое перемещение в начертательной геометрии называют плоско-параллельным), поэтому в итоге высота точек А' и В' над плоскостью П1 не изменилась. По этой причине линии, соединяющие на рис.20в точки А2 и A2', а также В2 и В2', - есть линии горизонтальные. То же происходит и на эпюре, а значит, для нахождения точек А2'В2' через А2 и В2 достаточно провести горизонтальные линии связи до их пересечения с соответствующими вертикальными линиями связи. А2'В2' - есть искомая натуральная величина отрезка АВ. В рассмотренном случае она получена методом вращения за счет того, что отрезок общего положения АВ был повернут параллельно одной из плоскостей проекций. Итак, сущность метода вращения состоит в том, что при неизменном положении плоскостей проекций изображаемый объект поворачивается в положение, удобное для решения задачи.
 Метод замены плоскостей проеций
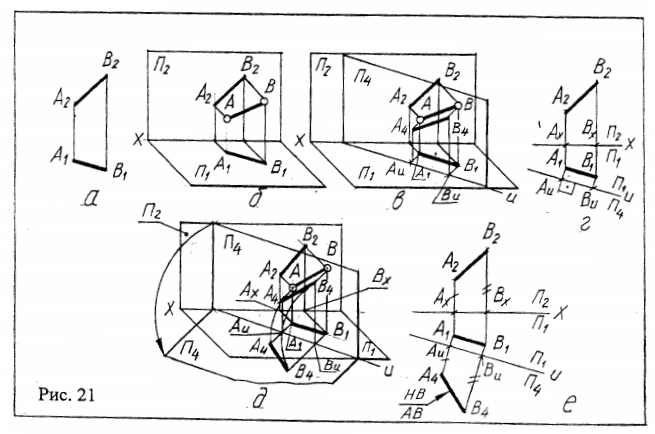
Вы заметили, что отрезок спроецируется на плоскость в натуральную величину, если он ей параллелен. Однако этого можно достичь не только соответствующим поворотом отрезка, но и подбором новой плоскости, параллельной ему. Эта операция называется заменой плоскостей проекций. Перед нами то же первоначальное фактическое условие задачи /рис.21а/. Для начала представим себе, как изобразить на рисунке плоскость, параллельную АВ /рис.216/. Ее можно расположить за отрезком АВ или перед ним. В последнем случае для построений больше свободного места. Теперь представьте, есть ли на рисунке ориентир, помогающий выбрать правильный поворот плоскости. Да, им является A1B1. Новая плоскость проекций, параллельная АВ и перпендикулярная П1 показана на рис.21 в. Будем считать, что она прозрачна, а потому за ней видны отрезок АВ и его проекции. Назовем построенную плоскость П4, т.к. индекс 3 закреплен за профильной плоскостью проекций, которая иногда используется при решении задач. А сейчас нам нужно спроецировать АВ на П4 перпендикулярно к ней. Направление, которое можно считать таким, представить довольно трудно, поэтому выберем его произвольно с единственным условием: оно не должно совпадать с направлением самого отрезка АВ. Известным нам способом /рис. 18/ спроецируем АВ на П4 /рис.21в/. Повторим те же построения на эпюре /рис.21 г/. Проведем ось U (она является горизонтальной проекцией П4) параллельно А1В1 и направим линии связи из точек А1 и B1 под прямым углом к U. Формально AUBU является проекцией АВ на П4, однако никак не может быть его натуральной величиной, пока П4, не будет повернута вокруг оси U совмещена с П1. То, что при этом произойдет, показано на рис.21 д. Представим, как должна изобразиться П4 на рисунке после ее поворота вокруг оси U до совмещения с П1. Легко представить, что после поворота все линии, которые были до этого вертикальными, станут параллельны направлению проецирования, осуществлявшемуся из точек А и В на П4. Таким образом, А4Аu станет продолжением A1Au, а В4Вu- продолжением В1Вu. Поскольку высота точек А и В над П1 при введении новой плоскости П4 осталась неизменной, эти величины соответственно равны А2АХ и В2ВХ. Однако заданный нам эпюр отрезка - безосный, поэтому для получения этих величин необходимо ввести ось X /рис.21 е/. Ее можно расположить на любой высоте, т.к. это не изменит конечного результата и не скажется на искомой НВ отрезка. Теперь от точек Аи и Вu отметим соответственно А2АХ и В2ВХ. А4В4 - есть искомая натуральная величина отрезка АВ. Запомним, что при решении задач с использованием метода замены плоскостей проекций желательно использовать осевой эпюр, т.к. меняя плоскость проекций П2 на П4, мы меняем систему П2/П1 на П1/П4. Эти обозначения должны присутствовать на эпюре. В заключение отметим: сущность метода замены плоскостей проекций состоит в том, что при неизменном положении изображаемого объекта подбирается новая плоскость, на которую объект проецируется в удобном для решения задачи виде.
Метод замены плоскостей проеций
Вы заметили, что отрезок спроецируется на плоскость в натуральную величину, если он ей параллелен. Однако этого можно достичь не только соответствующим поворотом отрезка, но и подбором новой плоскости, параллельной ему. Эта операция называется заменой плоскостей проекций. Перед нами то же первоначальное фактическое условие задачи /рис.21а/. Для начала представим себе, как изобразить на рисунке плоскость, параллельную АВ /рис.216/. Ее можно расположить за отрезком АВ или перед ним. В последнем случае для построений больше свободного места. Теперь представьте, есть ли на рисунке ориентир, помогающий выбрать правильный поворот плоскости. Да, им является A1B1. Новая плоскость проекций, параллельная АВ и перпендикулярная П1 показана на рис.21 в. Будем считать, что она прозрачна, а потому за ней видны отрезок АВ и его проекции. Назовем построенную плоскость П4, т.к. индекс 3 закреплен за профильной плоскостью проекций, которая иногда используется при решении задач. А сейчас нам нужно спроецировать АВ на П4 перпендикулярно к ней. Направление, которое можно считать таким, представить довольно трудно, поэтому выберем его произвольно с единственным условием: оно не должно совпадать с направлением самого отрезка АВ. Известным нам способом /рис. 18/ спроецируем АВ на П4 /рис.21в/. Повторим те же построения на эпюре /рис.21 г/. Проведем ось U (она является горизонтальной проекцией П4) параллельно А1В1 и направим линии связи из точек А1 и B1 под прямым углом к U. Формально AUBU является проекцией АВ на П4, однако никак не может быть его натуральной величиной, пока П4, не будет повернута вокруг оси U совмещена с П1. То, что при этом произойдет, показано на рис.21 д. Представим, как должна изобразиться П4 на рисунке после ее поворота вокруг оси U до совмещения с П1. Легко представить, что после поворота все линии, которые были до этого вертикальными, станут параллельны направлению проецирования, осуществлявшемуся из точек А и В на П4. Таким образом, А4Аu станет продолжением A1Au, а В4Вu- продолжением В1Вu. Поскольку высота точек А и В над П1 при введении новой плоскости П4 осталась неизменной, эти величины соответственно равны А2АХ и В2ВХ. Однако заданный нам эпюр отрезка - безосный, поэтому для получения этих величин необходимо ввести ось X /рис.21 е/. Ее можно расположить на любой высоте, т.к. это не изменит конечного результата и не скажется на искомой НВ отрезка. Теперь от точек Аи и Вu отметим соответственно А2АХ и В2ВХ. А4В4 - есть искомая натуральная величина отрезка АВ. Запомним, что при решении задач с использованием метода замены плоскостей проекций желательно использовать осевой эпюр, т.к. меняя плоскость проекций П2 на П4, мы меняем систему П2/П1 на П1/П4. Эти обозначения должны присутствовать на эпюре. В заключение отметим: сущность метода замены плоскостей проекций состоит в том, что при неизменном положении изображаемого объекта подбирается новая плоскость, на которую объект проецируется в удобном для решения задачи виде.
Оба рассмотренных нами метода (вращения и замены плоскостей проекций) являются
методами преобразования эпюра и преследуют одну и ту же цель - преобразовать исходные графические данные, чтобы упростить решение задачи.
Просмотры: 5840 |
Статью добавил:
slava191 |
Категория:
начертательная_геометрия



