Производные первого порядка
- Дифференцирование неявных функций
- Дифференцирование функций заданных параметрически
- Логарифмическое дифференцирование
- Приложения производной
Дифференцирование неявных функций.
Пусть значения переменных x и y связаны между собой некоторым уравнением, которое, если все его члены перенести в левую часть, может быть записано в виде F(x,y) = 0, где F(x,y)- некоторая функция двух переменных. Если для каждого значения х, принадлежащего некоторому множеству X, существует одно значение у, принадлежащее некоторому множеству Y, такое, что F(x,y) = 0, то этим определяется некоторая функция у = у(х). Такая функция называется неявной функцией, заданной уравнением F(x, y) = 0. Тогда F(x, y) = 0 (∀x∈X) => F'x(x, y(x)) = 0.
Дифференцирование функций заданных параметрически.
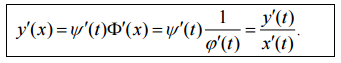
Полученная формула дает возможность находить производную функции, заданной параметрически, без определения непосредственной зависимости у от х.
Логарифмическое дифференцирование.
Иногда полезно использовать так называемую формулу логарифмического дифференцирования. Пусть f(х) > 0 на некотором множестве значений аргумента и дифференцируема на этом множестве. Тогда по формуле производной сложной функции имеем (ln f(x))' = f'(x) / f(x), откуда
f'(x) = f(x)(ln f(x))'
Приложения производной
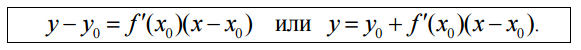

Углом между двумя кривыми
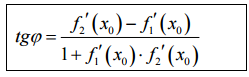
ЗАДАЧА 3761 Продифференцировать функцию, используя
Продифференцировать функцию, используя правило логарифмического дифференцирования: y=(cosx)^(sin2x) Смотреть решение...
ЗАДАЧА 3762 Продифференцировать функцию, заданную
Продифференцировать функцию, заданную параметрически: x=acos^3t, y=bsin^3t Смотреть решение...
ЗАДАЧА 3763 Продифференцировать функцию, заданную
Продифференцировать функцию, заданную неявно: x^2 + y^2 = 4 Смотреть решение...
ЗАДАЧА 3764 Под каким углом кривая y=lnx пересекает
Под каким углом кривая y=lnx пересекает ось Ox
Смотреть решение...
Просмотры: 2942 |
Статью добавил: slava191 |
Категория: математический_анализ
☰ Меню