Векторная алгебра Часть II
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение трех векторов
Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Если угол между векторами vector{a}, vector{b} обозначить через phi, то их скалярное произведение можно выразить формулой
Скалярное произведение vector{a}vector{a} называется скалярным квадратом вектора и обозначается символом vector{a}^2. Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
то их скалярное произведение может быть вычислено по формуле
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
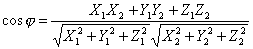
Проекция произвольного вектора S = {X;Y;Z} на какую-нибудь ось u определяется формулой
ЗАДАЧА 3758 Вычислив внутренние углы треугольника с
Вычислив внутренние углы треугольника с вершинами A(1; 2; 1), B(3; -1; 7), C(7; 4; -2), убедиться, что этот треугольник равнобедренный. Смотреть решение...
Векторное произведение векторов
1) Модуль вектора [vector{a}vector{b}] равен |vector{a}||vector{b}|sinphi, где phi - угол между векторами vector{a} и vector{b} ;
2) Вектор [vector{a}vector{b}] перпендикулярен к каждому из вектора vector{a} и vector{b} ;
3) Направление вектора [vector{a}vector{b}] соответствует «правилу правой руки». Это означает, что если векторы vector{a}, vector{b} и [vector{a}vector{b}] приведены к общему началу, то вектор [vector{a}vector{b}] должен быть направлен так, как направлен средний палец правой руки, большой палец которой направлен по первому сомножителю (то есть по вектору vector{a}), а указательный - по второму (то есть по вектору vector{b}).
Векторное произведение зависит от порядка сомножителей, именно:
Само векторное произведение может быть выражено формулой
Векторное произведение [vector{a}vector{b}] обращается в нуль тогда и только тогда, когда векторы vector{a} и vector{b} коллинеарны. В частности, [vector{a}vector{a}] = 0.
Если система координатных осей правая и векторы vector{a} и vector{b} заданы в этой системе своими координатами:
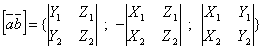
или
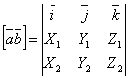
ЗАДАЧА 3759 Даны точки А(1; 2; 0), В(3; 0; -3), С(5;
Даны точки А(1; 2; 0), В(3; 0; -3), С(5; 2; 6). Вычислить площадь треугольника АВС. Смотреть решение...
Смешанное произведение трех векторов
Тройка некомпланарных векторов vector{a}, vector{b}, vector{c} называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы vector{a}, vector{b}, vector{c} расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.
Смешанным произведением трех векторов vector{a}, vector{b}, vector{c} называется число, равное векторному произведению [vector{a}vector{b}], умноженному скалярно на вектор vector{c}, то есть [vector{a}vector{b}]vector{c}.
Имеет место тождество [vector{a}vector{b}]vector{c} = vector{a}[vector{b}vector{c}], ввиду чего для обозначения смешанного произведения [vector{a}vector{b}]vector{c} употребляется более простой символ vector{a}vector{b}vector{c}. Таким образом,
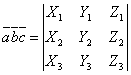
ЗАДАЧА 3760 Даны вершины тетраэдра A(2; 3; 1), B(4;
Даны вершины тетраэдра A(2; 3; 1), B(4; 1; -2), C(6; 3; 7), D(-5; -4; 8). Найти длину его высоты, опущенной из вершины D. Смотреть решение...
Просмотры: 3555 |
Статью добавил: slava191 |
Категория: аналитическая_геометрия
☰ Меню