Сочетания
Схема выбора, приводящая к сочетаниям. Если опыт состоит в выборе m элементов без возвращения и без упорядочивания, то различными исходами следует считать m-элементные подмножества множества Е, имеющие различный состав. Получаемые при этом комбинации элементов (элементарные исходы) носят название сочетания из n элементов по m , а их общее число N(Ω) определяется по формуле
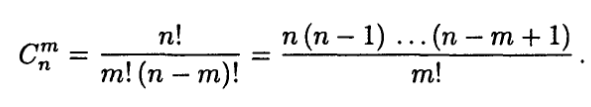
Для чисел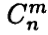 , называемых также биномиальными коэффициентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач:
, называемых также биномиальными коэффициентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач:

Пример. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятности следующих событий: А = {в полученной выборке ровно одно изделие бракованное}, В = {в полученной выборке нет ни одного бракованного изделия}.
Занумеруем изделия числами от 1 до 10, и пусть множество номеров Е1 = {1, 2, ..7} соответствует годным изделиям, а множество номеров E2 = {8, 9, 10} — бракованным изделиям.
Согласно описанию эксперимента производится выбор без возвращения и без упорядочивания трех элементов из множества Е = E1 U Е2 = {1, 2, ..., 10}. Поэтому
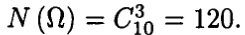
Событию А благоприятствуют только такие исходы, когда один элемент выборки принадлежит Е2, а остальные два элемента — множеству Е1. По формуле прямого произведения множеств получаем, что число всех таких исходов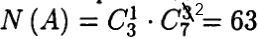 , поэтому
, поэтому
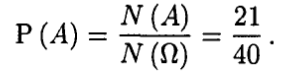
Событию В благоприятствуют только такие исходы, когда все три отобранных элемента принадлежат множеству E1, поэтому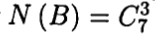 . Отсюда следует, что
. Отсюда следует, что
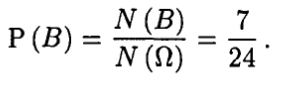
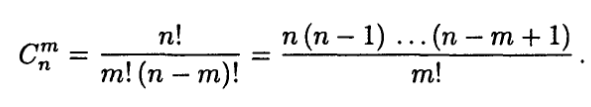
Для чисел
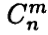 , называемых также биномиальными коэффициентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач:
, называемых также биномиальными коэффициентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач:
Пример. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятности следующих событий: А = {в полученной выборке ровно одно изделие бракованное}, В = {в полученной выборке нет ни одного бракованного изделия}.
Занумеруем изделия числами от 1 до 10, и пусть множество номеров Е1 = {1, 2, ..7} соответствует годным изделиям, а множество номеров E2 = {8, 9, 10} — бракованным изделиям.
Согласно описанию эксперимента производится выбор без возвращения и без упорядочивания трех элементов из множества Е = E1 U Е2 = {1, 2, ..., 10}. Поэтому
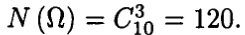
Событию А благоприятствуют только такие исходы, когда один элемент выборки принадлежит Е2, а остальные два элемента — множеству Е1. По формуле прямого произведения множеств получаем, что число всех таких исходов
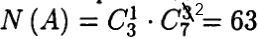 , поэтому
, поэтому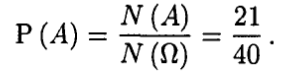
Событию В благоприятствуют только такие исходы, когда все три отобранных элемента принадлежат множеству E1, поэтому
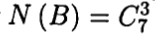 . Отсюда следует, что
. Отсюда следует, что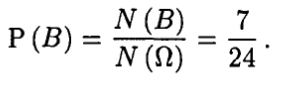
Просмотры: 7204 |
Статью добавил: slava191 |
Категория: теория_вероятностей
☰ Меню