Дифференцирование функций
- Производная
- Геометрический смысл производной
- Механический смысл производной
- Необходимое условие существования производной
- Основные правила дифференцирования
- Таблица производных
Производная
Определение. Производной функции y=f(x) в точке
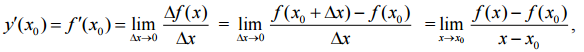
если этот предел существует и конечен (если предел бесконечен, то иногда говорят про бесконечную производную).
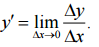
Геометрический смысл производной
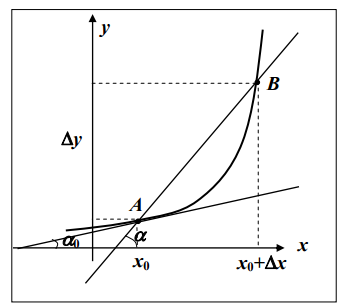
Рассмотрим график функции у = f(х) и проведем секущую через точки А с абсциссой
Если Δх —> 0, точка В перемещается по кривой, приближаясь к точке А, и секущая при совпадении точек В и А превращается в касательную к графику функции, образующую с осью Ох угол a0.
При этом
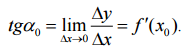
Значение производной при данном значении х равно тангенсу угла, образованного касательной к графику функции в точке с соответствующим значением х с положительным направлением оси Ох.
Механический смысл производной
Рассмотрим прямолинейное движение тела, для которого пройденное расстояние есть функция от времени: s = f(t). Среднюю скорость за время Δt можно определить по формуле: Vcp = Δs/Δt
Для определения мгновенной скорости тела в данный момент времени Δt к нулю. Получим:
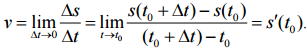
Таким образом, производная от расстояния в данный момент времени равна мгновенной скорости движения в этот момент. Соответственно,
Производная любой функции при данном значении аргумента равна скорости изменения этой функции при рассматриваемом х.
Необходимое условие существования производной
Теорема.
Основные правила дифференцирования

Теорема. (Производная обратной функции).
Теорема о производной сложной функции.
Таблица производных
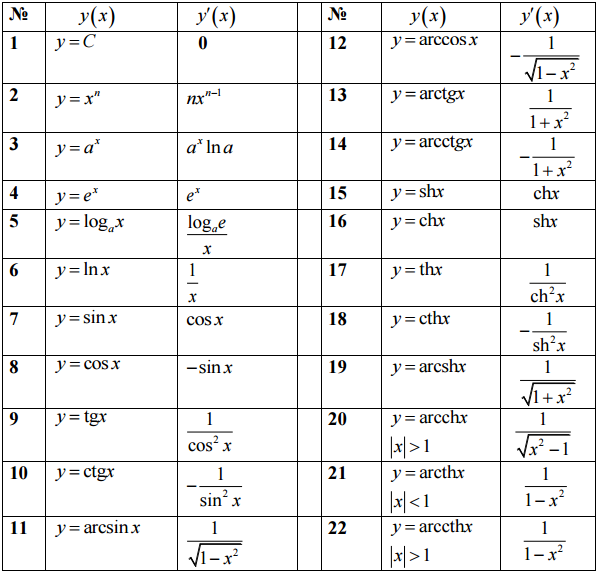
ЗАДАЧА 3721 Продифференцировать функцию y=arcsinx/x
Продифференцировать функцию y=arcsinx/x Смотреть решение...
Просмотры: 9180 |
Статью добавил: slava191 |
Категория: математический_анализ
☰ Меню