Проецирование точки на две плоскости проекций

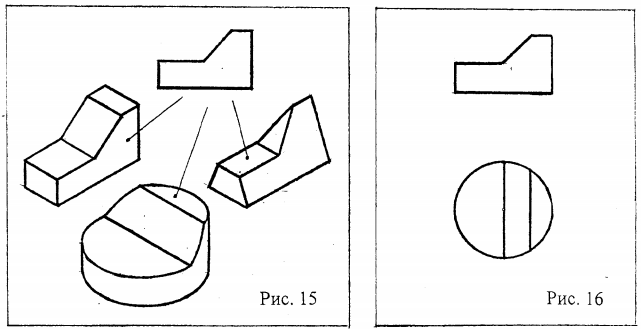
Представим, что фигура, изображенная на рис. 15, является проекцией конкретного объекта. Можно ли на основе этой одной проекции судить о его форме? Конечно нет, ибо любой из предметов, показанных рядом, изображается заданной проекций, хотя их форма различна. Но если рядом поместить изображение объекта с другой стороны, то сравнивая его с заданным, можно определить форму объекта более точно или вообще однозначно /рис. 16/. Последнее означает, что чертеж становится обратимым, т.е. достаточным для представления по нему (реконструкции) формы объекта. Сделаем вывод: форма трехмерного (объемного) объекта одной проекцией без дополнительных пояснений не определяется.



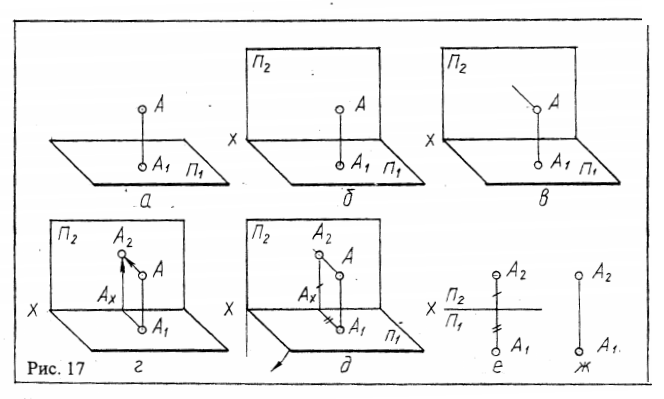
Для того, чтобы понять, где именно и почему одна проекция объекта должна быть расположена на чертеже по отношению к другой, рассмотрим это на примере точки. На рис. 17а показана точка А, спроецированная на П1. Введем новую плоскость П2, расположенную под прямым углом к П1 и называемую фронтальной плоскостью проекций. Линией пересечения П1 и П2 является ось X /рис. 176/. Спроецируем точку А на П1. Для этого направим через А луч, перпендикулярный П2 /рис.17в/. Чтобы найти фронтальную проекцию точки А, проведем через А1 линию связи, параллельную уже имеющемуся лучу, т.е. перпендикулярно П2, а затем через Аx - линию связи АxА2 перпендикулярно X. Тем самым определится А2 - фронтальная проекция точки А. Мы получили изображение точки А в системе двух плоскостей проекций /рис.17г/. После этого две плоскости проекций обычно совмещает в одну за счет того, что поворачивают П1 вокруг оси X до совмещения с П2 /рис.17д/. После совмещения плоскостей проекций нет смысла показывать ограничивающие их фигуры. Просто отметим, что плоскость, расположенная ниже оси X,- есть П1 а плоскость, расположенная выше оси X, - П2 /рис. 17е/. Теперь от любой точки Ах отметим на перпендикулярных к оси X линиях связи отрезки АxА1 и АxА2. Эти отрезки соответствуют расстояниям от точки А до плоскостей проекций П1 и П2. Плоскйй чертеж, полученный путем совмещения плоскостей проекций, называется эпюром . Таким образом, на эпюре полнота данных о положении точки в системе плоскостей проекций соответствует этим же сведениям на наглядном изображении. Эпюр, приведенный на рис.17е, называется осевым эпюром точки, однако эпюр может быть и безосным /рис.17ж/. На безосном эпюре нельзя определить расстояний от точки до плоскостей проекций, однако на практике такая задача обычно и не ставится. В черчении важнее оказываются расстояния между проекциями точек или других элементов, образующих очертание проекций фигуры /см. рис. 16/. Рассмотрев закономерности расположения проекций точки на эпюре, мы легко можем объяснить проекционную взаимосвязь изображений на техническом чертеже и, в частности, то, что вид сверху располагается точно под видом спереди.