Непрерывность функций
- Непрерывность функции в точке
- Основные теоремы о непрерывных функциях
- Односторонняя непрерывность
- Непрерывность и разрывы монотонной функции
Непрерывность функции в точке
Определение. Пусть функция у = f(x) определена в точке
1. существует
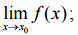
2. этот предел равен значению функции в точке x0:
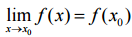
Определение.
Определение.
Определение. Функция f(х), не являющаяся непрерывной в точке x0, называется разрывной в этой точке.
Определение. Функция f(х) называется непрерывной на множестве X, если она непрерывна в каждой точке этого множества.
Основные теоремы о непрерывных функциях
Теорема о непрерывности суммы, произведения, частного

Теорема о переходе к пределу под знаком непрерывной функции

Теорема о непрерывности суперпозиции непрерывных функций

Односторонняя непрерывность

Непрерывность и разрывы монотонной функции
Пусть функция f(x) определена на отрезке [a,b] и монотонна на этом отрезке. Тогда f(x) может иметь на этом отрезке только точки разрыва первого рода.
Теорема о промежуточном значении. Если функция f(x) непрерывна на отрезке и в двух точках а и b (a меньше b) принимает неравные значения A = f(a) ≠ В = f(b), то для любого числа С, лежащего между А и В, найдётся точка c ∈ [a,b], в которой значение функции равно С: f(c) = C.
Теорема об ограниченности непрерывной функции на отрезке. Если функция f(x) непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема о достижении минимального и максимального значений. Если функция f(x) непрерывна на отрезке, то она достигает на этом отрезке свои нижнюю и верхнюю грани.
Теорема о непрерывности обратной функции. Пусть функция y=f(x) непрерывна и строго возрастает (убывает) на отрезке [а,b]. Тогда на отрезке [m, M] существует обратная функция х = g(y), также монотонно возрастающая (убывающая) на [m, M] и непрерывная.
Просмотры: 15634 |
Статью добавил: slava191 |
Категория: математический_анализ
☰ Меню