• Ось и отрезок оси. Координаты на прямой


• Декартовы прямоугольные координаты на плоскости


• Полярные координаты


• Отрезок, его проекции, длина, полярный угол. Расстояние между двумя точками


• Деление отрезка в данном отношении


• Площадь треугольника


• Преобразование координат

Ось и отрезок оси. Координаты на прямой

Прямая, на которой выбрано положительное направление, называется осью. Отрезок оси, ограниченный какими-нибудь точками A и B, называется направленным, если сказано, какая из этих точек считается началом отрезка, какая – концом. Направленный отрезок с началом A и концом B обозначается символом AB. Величиной направленного отрезка оси называется его длина, взятая со знаком плюс, если направление отрезка (т.е. направление от начала к концу) совпадает с положительным направлением оси, и со знаком минус, если это направление противоположно положительному направлению оси. Величина отрезка AB обозначается символом AB, его длина – символом |AB|. Если точки A и B совпадают, то определяемый ими отрезок называется нулевым; очевидно, в этом случае АВ = ВА = 0 (направление нулевого отрезка следует считать неопределенным).

Пусть дана произвольная прямая а. Выберем некоторый отрезок в качестве единицы измерения длин, назначим на прямой а положительное направление (после чего она становится осью) и отметим на этой прямой буквой О какую-нибудь точку. Тем самым на прямой а будет введена система координат.

Координатой любой точки М прямой а (в установленной системе координат) называется число x, равное величине отрезка ОМ:



Точка О называется началом координат; ее собственная координата равна нулю. В дальнейшем символ М(х) означает, что точка М имеет координату х.

Если M1(x1) и M2(x2) - две произвольные точки прямой а, то формула



выражает величину отрезка M1M2, формула



выражает его длину.

Декартовы прямоугольные координаты на плоскости

Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке.

Точка пересечения осей называется началом координат, а сами оси - координатными осями. Первая из координатных осей называется осью абсцисс, вторая - осью ординат.

Начало координат обозначается буквой О, ось абсцисс - символом Ох, ось ординат - символом Оу.

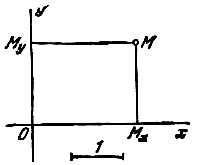
Координатами произвольной точки М в заданной системе называют числа



где Mx и My суть проекции точки М на оси Ох и Оу, OMx обозначает величину отрезка OMx оси абсцисс, OMy - величину отрезка OMy оси ординат. Число х называется абсциссой точки М, число у - ординатой этой же точки. Символ М(х; у) обозначает, что точка М имеет абсциссой число х, а ординатой число у.



Ось Оу разделяет всю плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Ох, называется правой, другая - левой. Точно так же ось Оу разделяет плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Оу, называется верхней, другая нижней.

Обе координатные оси вместе разделяют плоскость на четыре четверти, которые нумеруют по следующему правилу: первой координатной четвертью называется та, которая лежит одновременно в правой и в верхней полуплоскости, второй - лежащая в левой и в верхней полуплоскости, третьей - лежащая в левой и в нижней полуплоскости, четвертой - лежащая в правой и в нижней полуплоскости.

Полярные координаты

Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча ОА, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

Полярными координатами произвольной точки М (относительно заданной системы) называются числа p=OM и ТЕТА=уголAOM (см. рис.). Угол ТЕТА при этом следует понимать так, как принято в тригонометрии. Число p называется первой координатой, или полярным углом точки М (ТЕТА называются также амплитудой).



Символ М(p; ТЕТА) обозначает, что точка М имеет полярные координаты p и ТЕТА.

Полярный угол ТЕТА имеет бесконечно много возможных значений (отличающихся друг от друга на величину вида +-2Pin, где n - целое положительное число). Значение полярного угла, удовлетворяющее неравенствам -Pi<ТЕТА<+Pi, называется главным.

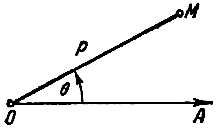
В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1). Пользоваться одним и тем же масштабом, 2). При определении полярных углов считать положительным повороты в том направлении, в каком следует вращать положительную ось абсцисс, чтобы кратчайшим путем совместить ее с положительной осью ординат (таким образом, если оси декартовой системы находятся в обычном расположении, то есть ось Ох направлена вправо, а ось Оу - вверх, то и отсчет полярных углов должен быть обычным, то есть положительными следует считать те углы, которые отсчитываются против часовой стрелки).

При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки х к декартовым координатам той же точки осуществляется по формулам



В этом же случае формулы



являются формулами перехода от декартовых координат к полярным.

При одновременно рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштаб для обеих систем одинаковыми.

Направленный отрезок. Проекция отрезка на произвольную ось. Проекция отрезка на координатные оси. Длина и полярный угол отрезка. Расстояние между двумя точками

Прямолинейный отрезок называется направленным, если указано, какая из ограничивающих его точек считается началом, какая - концом. Направленный отрезок, имеющий точку А своим началом и точку В концом (см. рис.), обозначается символом AB (то есть так же, как отрезок оси). Длина направленного отрезка AB (при заданном масштабе) обозначается символом |AB| (или АВ).



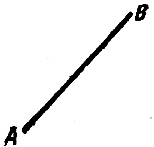
Проекцией отрезка AB на ось u называется число, равное величине отрезка A1B1 оси u, где точка A1 является проекцией точки А на ось u, а точка B1 - проекцией точки В на эту же ось.

Проекция отрезка AB на ось u обозначается символом ПРаAB. Если на плоскости задана система декартовых прямоугольных координат, то проекция отрезка на ось Ох обозначается символом Х, его проекция на ось Оу - символом Y.

Если известны координаты точек M1(x1, y1) и M2(x2, y2), то проекции X и Y направленного отрезка M1M2 на координатные оси могут быть вычислены по формулам



Таким образом, чтобы найти проекции направленного отрезка на координатные оси, нужно от координат его конца отнять соответствующие координаты начала.

Угол ТЕТА, на который нужно повернуть положительную полуось Ох так, чтобы ее направление совпало с направлением отрезка M1M2, называется полярным углом отрезка M1M2.

Угол ТЕТА понимается как в тригонометрии. Соответственно этому ТЕТА имеет бесконечно много возможных значений, которые отличаются друг от друга на величину вида +-2Pin (где n - целое положительное число). Главным значением полярного угла называется то из его значений, которое удовлетворяет неравенствам -Pi<ТЕТА меньше или равно +Pi.

Формулы



выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Отсюда же вытекают формулы



которые выражают длину и полярный угол отрезка через его проекции на координатные оси.

Если на плоскости даны две точки M1(x1, y1) и M2(x2, y2), то расстояние d между ними определяется формулой

Деление отрезка в данном отношении

Если точка М(x; y) лежит на прямой, проходящей через две данные точки M1(x1, y1) и M2(x2, y2), и дано отношение лямбда = M1M/MM2, в котором точка М делит отрезок M1M2, то координаты точки М определяются по формулам



Если точка М является серединой отрезка M1M2, то ее координаты определяются по формулам

Площадь треугольника

Каковы бы ни были три точки A(x1; y1), B(x2; y2), C(x3; y3), площадь S треугольника ABC дается формулой



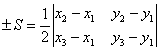
Правая часть этой формулы равна +S в том случае, когда кратчайший поворот отрезка AB к отрезку AC положителен, и -S в том случае, когда такой поворот отрицателен.

Преобразование координат

Преобразование декартовых координат при параллельном сдвиге осей определяется формулами



Здесь x, y - координаты произвольной точки М плоскости относительно старых осей, x', y' - координаты той же точки относительно новых осей, a, b - координаты нового начала O' относительно старых осей (говорят также, что a - величина сдвига в направлении оси абсцисс, b - величина сдвига в направлении оси ординат).

Преобразование декартовых прямоугольных координат при повороте осей на угол альфа(который надо понимать, как в тригонометрии) определяется формулами



Здесь x, y суть координаты произвольной точки М плоскости относительно старых осей, x’, y’ - координаты той же точки относительно новых осей.

Формулы



определяют преобразование координат при параллельном сдвиге системы осей на величину а в направлении Ох, на величину b в направлении Оу и последующем повороте осей на угол a. Все указанные формулы соответствуют преобразованию координат при неизменном масштабе.